TI-83, TI-83 Plus, TI-84 Plus Guide
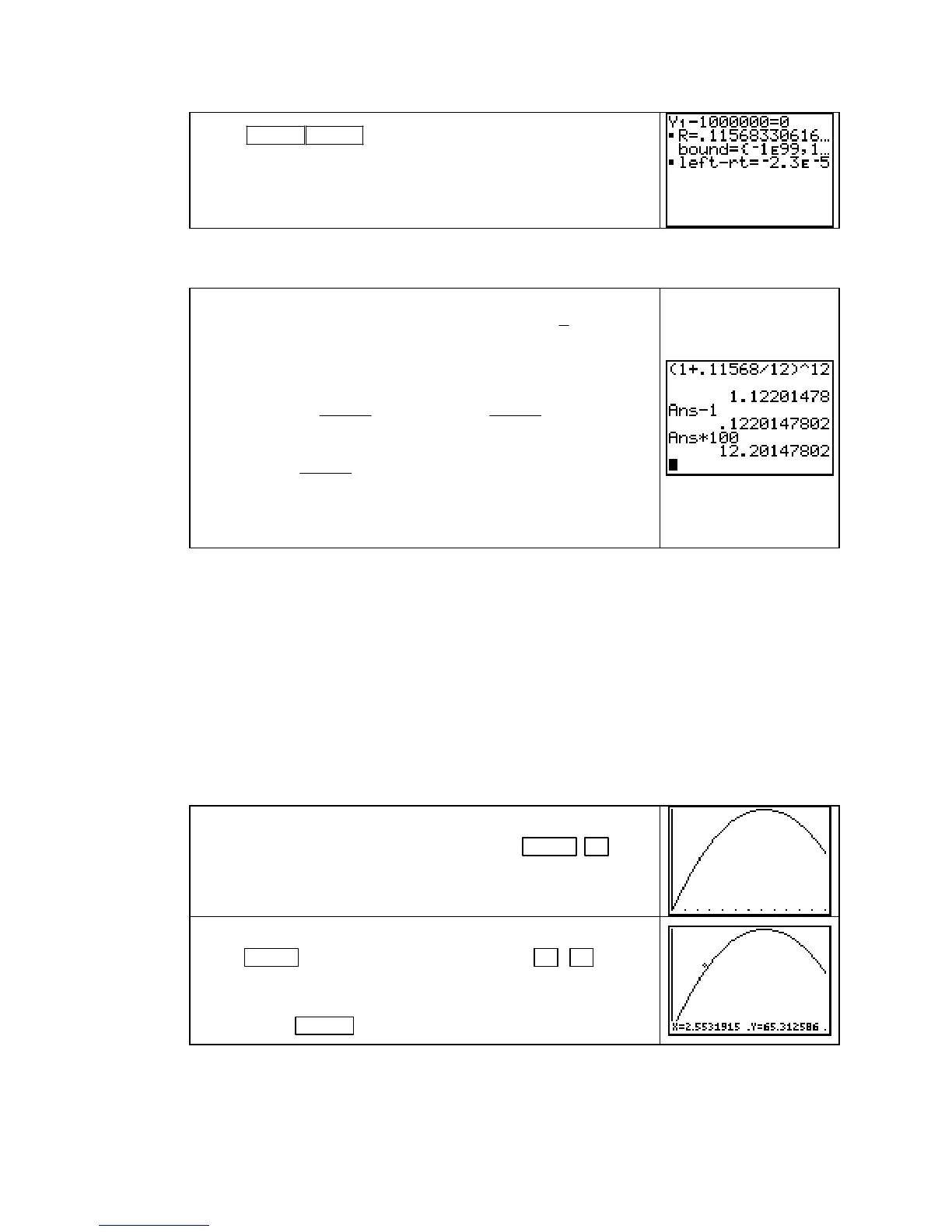
Press ALPHA ENTER . An APR of approximately 11.57%
compounded monthly will yield $1,000,000 in 40 years on an
initial investment of $10,000.
We continue with part b of Example 4 of Section 2.1 of Calculus Concepts to illustrate finding
the APY that corresponds to an APR of approximately 0.11568.
Substitute r = 0.11568 into the formula () 1
⎛⎞
=+
⎜⎟
⎝⎠
nt
r
At P
n
and
rewrite the formula in the form
()=
t
tab.
12 12
0.11568 0.11568
( ) 10,000 1 10,000 1
12 12
⎤
⎛⎞ ⎛⎞
=+ = +
⎥
⎜⎟ ⎜⎟
⎝⎠ ⎝⎠
⎥
⎦
t
t
At .
Evaluate
12
0.11568
1
12
⎡⎤
⎛
+
⎢
⎜
⎝⎠
⎢⎥
⎣⎦
⎞
⎥
⎟
on the home screen. Rewrite the
equation as
. The APY is (b-1)100% or
approximately 12.20%.
( ) 10,000(1.1220 )≈
t
At
2.2 Instantaneous Rates of Change
We first examine the principle of local linearity, which says that if you are close enough, the
tangent line and the curve are indistinguishable. We also explore two methods for using the
calculator to draw a tangent line at a point on a curve.
2.2.1 MAGNIFYING A PORTION OF A GRAPH The
ZOOM menu of your calculator allows
you to magnify any portion of a graph. Consider the graph shown in Figure 2.7 in Section 2.2
of Calculus Concepts. The temperature model is T(x) =
−
0.804x
2
+ 11.644x + 38.114 degrees
Fahrenheit where x is the number of hours after 6 a.m.
Enter the temperature equation in Y1 and draw the graph be-
tween 6 a.m. (x = 0) and 6 p.m. (x = 12) using
ZOOM ▲
[ZoomFit].
We now want to zoom and “box” in several points
on the graph to see a magnified view at those points.
The first point we consider on the graph is point A with x = 3.
Press
ZOOM 1 [ZBox] and use the arrow keys ( ◄ , ▲ , etc.)
to move the cursor to the left of the curve close to where x = 3.
(You may not have the same coordinates as those shown on the
right.) Press
ENTER to fix the lower left corner of the box.
Copyright © Houghton Mifflin Company. All rights reserved.
45
To Next Page
Loading...
Need help?
General
