Chapter 2
many decimal places as are necessary to determine the limit to the desired degree of
accuracy.
• Note: You may wish to leave the slope formula in Y2 as long as you need it. Turn Y2 off
when you are not using it.
2.4 Algebraically Finding Slopes
The calculator does not find algebraic formulas for slope, but you can use the built-in
numerical derivative and draw the graph of a derivative to check any formula that you find
algebraically.
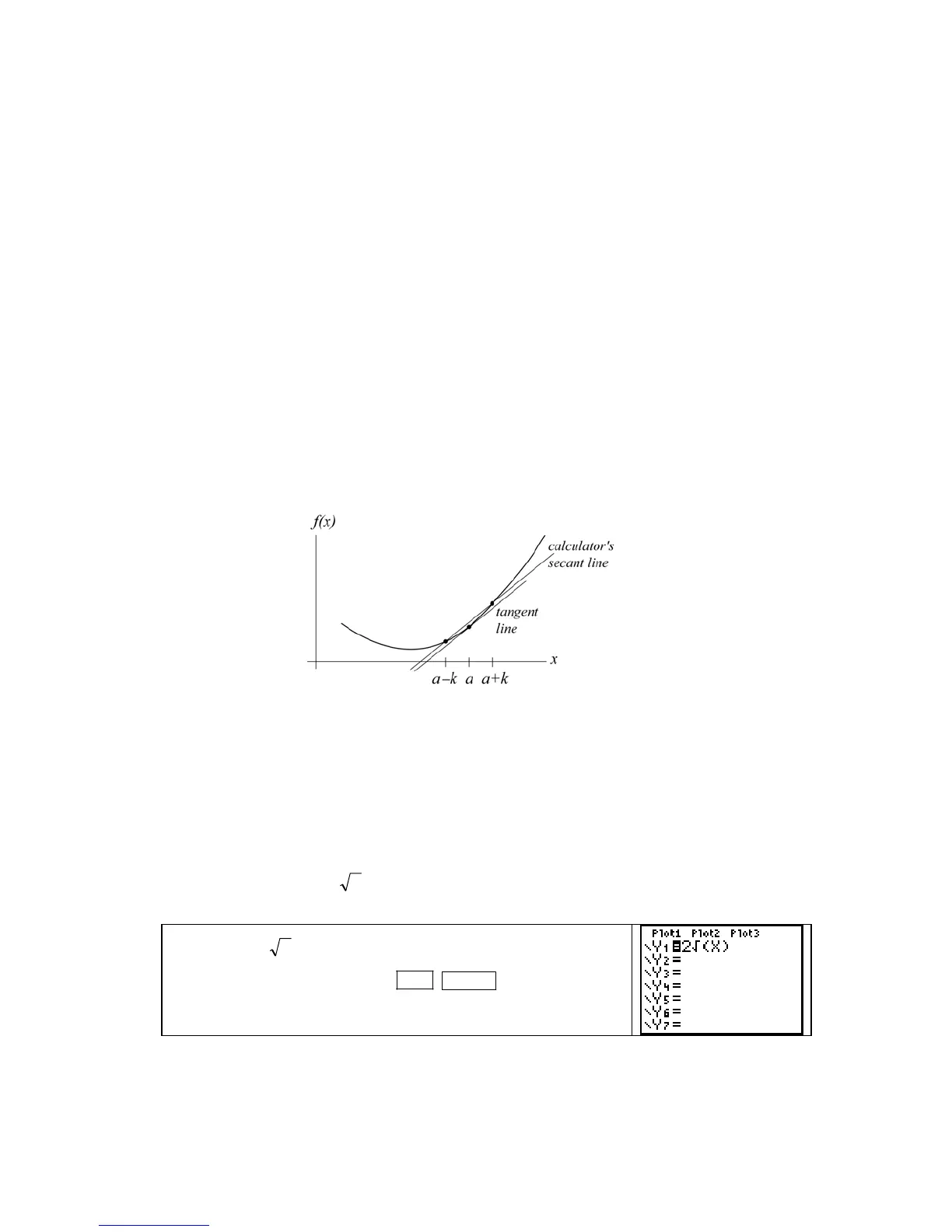
UNDERSTANDING YOUR CALCULATOR’S SLOPE FUNCTION
The calculator uses
the slope of a secant line to approximate the slope of the tangent line at a point on the graph of a
function. However, instead of using a secant line through the point of tangency and a close
point, the calculator uses the slope of a secant line through two close points that are equally
spaced from the point of tangency.
The secant line joining the points (a
−
k, f(a
−
k)) and (a + k, f(a + k)) and the line tangent
to the graph of f where x = a are shown in Figure 4. Notice that the slopes of the secant line
and tangent appear to be close to the same value even though these are different lines.
Figure 4
As k gets closer and closer to 0, the two points through which the secant line passes move
closer and closer to a. Provided the slope of the tangent line exists, the limiting position of the
secant line will be the tangent line.
The calculator’s notation for the slope of the secant line shown in Figure 4 is
nDeriv(function, symbol for input variable, a, k)
Specifying the value of k is optional. If a value for k is not given, the calculator automatically
uses k = 0.001. Any smooth, continuous function will do, so let’s investigate these ideas with
another function: f(x) =
2 x .
Enter f(x) = 2 x in one of the locations of the Y= list, say Y1.
Return to the home screen with
2ND MODE (QUIT).
Copyright © Houghton Mifflin Company. All rights reserved.
52
To Next Page
Loading...
Need help?
General
