TI-83, TI-83 Plus, TI-84 Plus Guide
AREA APPROXIMATIONS USING RIGHT RECTANGLES
We continue with the
previous function and find an area approximation using right rectangles.
Part a of Example 2 says to find the change in the drug concen-
tration from x = 0 through x = 20 using right rectangles of width
2 days. Enter the right endpoints
(2, 4, 6, …, 20) in L1.
Use the piecewise continuous function r in
Y3 (or use Y1) to
find the rectangle heights. As shown, enter the heights in
L2.
• Note that the heights in L2 are the values in Table 5.3 in the text, but the Table 5.3
values have been rounded for printing purposes.
Find the right-rectangle areas by multiplying each entry in
L2
by 2. This is the same as multiplying the sum of the heights by
2. On the home screen, press
2 U 2ND STAT (LIST) ►
►
[MATH] 5 [sum] 2ND 2 (L2) ) ENTER .
Part b of Example 2 asks us to use the model and right rectangles of width 2 days to estimate
the change in drug concentration from x = 20 to x = 30. Notice that the signed heights in
L4
are the same as those given in the text in Table 5.4 (except for rounding.)
Enter the right endpoints
(22, 24, 26, 28, 30) in L3.
Use the piecewise continuous function r in
Y3 (or use Y2) to
find the rectangle heights. As shown to the right, enter the
signed heights in
L4.
Find the signed right-rectangle areas by multiplying each entry
in
L2 by 2. This is the same as multiplying the sum of the signed
heights by 2. On the home screen, press
2ND ENTER
(ENTRY)
to return the sum instruction to the screen, change L2 to
L4 with ◄ ◄ and then type 2ND 4 (L4). Press ENTER .
AREA APPROXIMATIONS USING MIDPOINT RECTANGLES Areas of midpoint
rectangles are found using the same procedures as those used to find left and right rectangle
areas except that the midpoint of the base of each rectangle is entered in the first list and no
endpoints are deleted. We illustrate the midpoint-rectangle approximation using the function f
in Example 3 of Section 5.1 in Calculus Concepts.
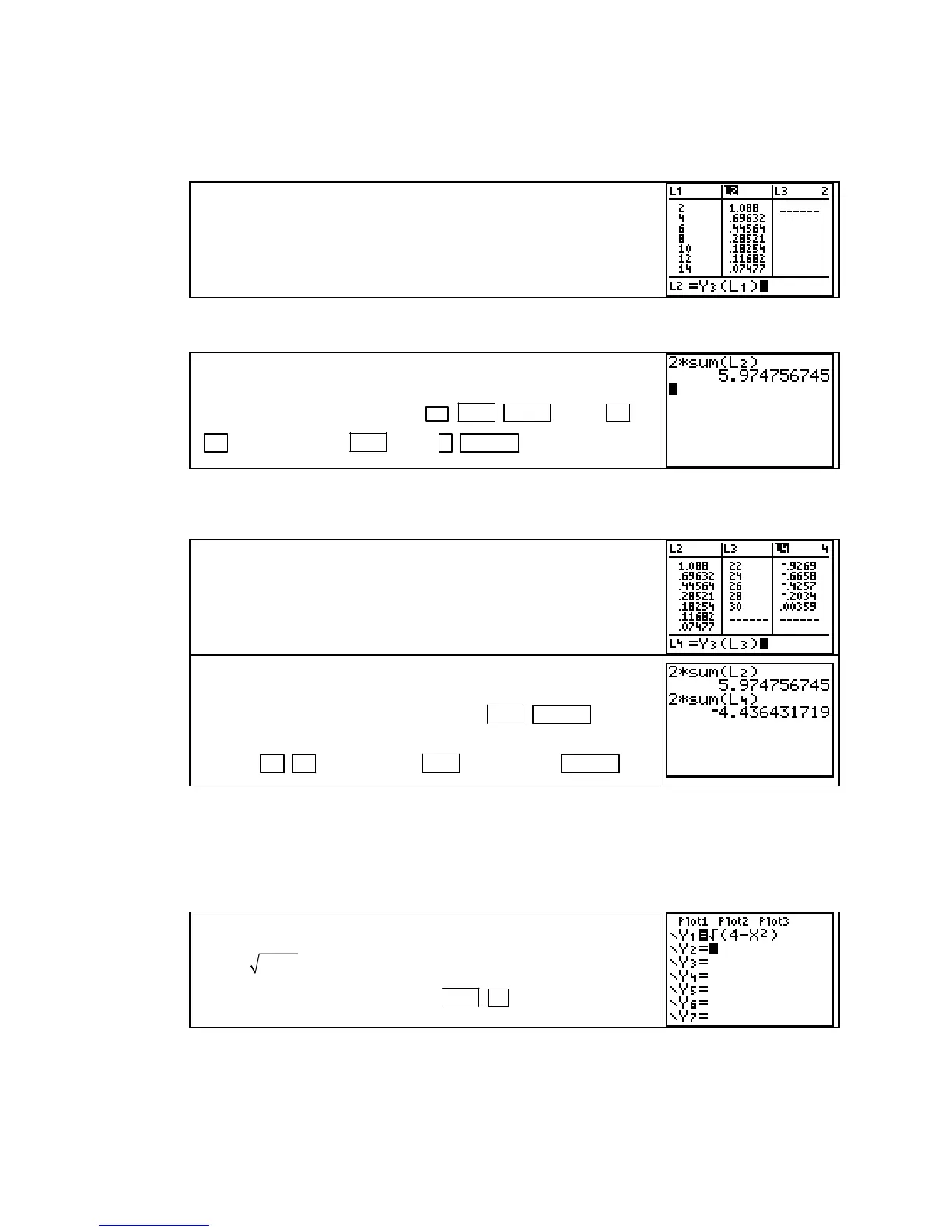
Clear all functions from the Y= list. Next, enter the function
f
(x) =
2
4
− in some location of the Y= list, say Y1.
(Type the square root symbol with
2ND x
2
.)
Copyright © Houghton Mifflin Company. All rights reserved.
69

 Loading...
Loading...

















