Chapter 1
Enter
Y1 + Y2 in Y3 to obtain the sum function (f + g)(x) = f(x) + g(x).
Enter
Y1 – Y2 in Y4 to obtain the difference function (f – g)(x) = f(x) – g(x).
Enter
Y1*Y2 in Y5 to obtain the product function (f
⋅
g)(x) = f(x)
⋅
g(x).
Enter
Y1/Y2 in Y6 to obtain the quotient function (f ÷ g)(x) =
fx
gx
()
()
.
Enter Y1(Y2) in Y7 to obtain the composite function (f
o
g)(x) = f(g(x)).
The functions can be entered in any location in the
Y= list. Although the calculator will not
give an algebraic formula for a constructed function, you can check your final answer by
evaluating your constructed function and the calculator-constructed function at several
different points to see if they yield the same outputs.
FINDING A DIFFERENCE FUNCTION We illustrate this technique with the functions for
Cost = C(x) = - 0.32x
2
+ 6x + 1030 dollars for the total cost of milk production on the x
th
day of
last month (found on p. 11 of Calculus Concepts) and Revenue = R(x) =
[]
(
0.02 1.90 1.5 0.5 0.8
x
x
⎡
+⋅+
⎣
⎤
⎦
thousand dollars revenue from the sale of milk on the x
th
day of
last month (found on p. 13 of Calculus Concepts). To construct a profit function, P(x), we must
subtract C(x) from R(x). Because the output of R(x) is thousand dollars, we divide C(x) by by
1000 so that our output units will be thousand dollars.
()
() ()
1000
Cx
Px Rx=− thousand dollars on
the x
th
day of last month.
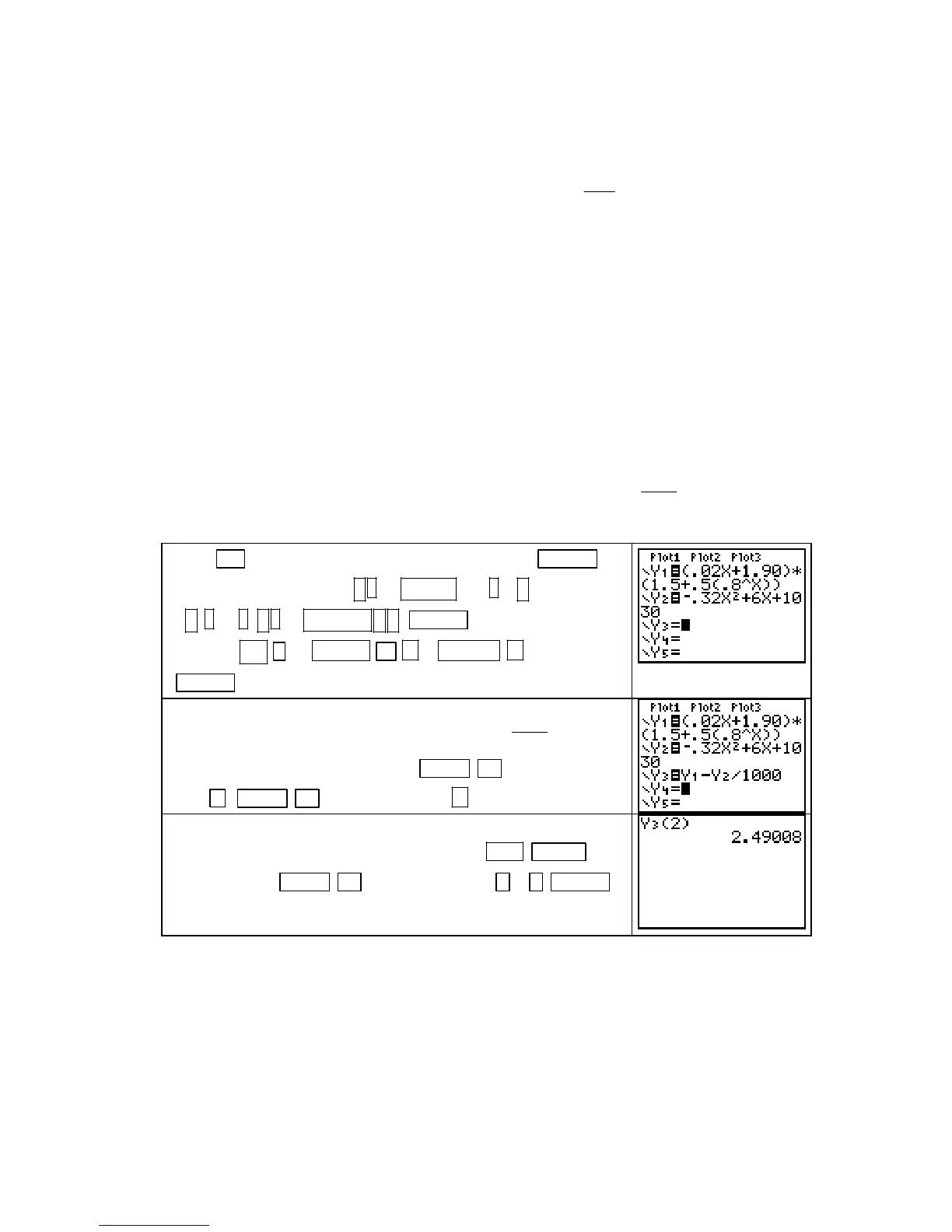
Press Y= . Clear previously entered equations with CLEAR .
Enter R in Y1 by pressing ( . 02 X,T, ,n 1. 90 )+
* ( 1 . 5 . 5 ( . 8 ^ X,T, ,n ) )+ ENTER and enter C in Y2 by
pressing
(-) . 32 X,T,θ,n x
2
6 X,T,θ,n
1030
ENTER
The difference function, the profit P(x) =
()
()
1000
Cx
Rx
− =
Y1 – Y2/1000, is entered in Y3 with VARS ► 1 [Function] 1
[Y1]
− VARS ► 1 [Function] 2 [Y2]
1000.
To find the profit in on the 2
nd
day of last month, evaluate Y3
when
X = 2. Return to the home screen with 2ND MODE
(QUIT).
Press VARS ► 1 [Function] 3 [Y3] ( 2 ) ENTER
to see the result. We find that the profit on the 2
nd
day of last
month was approximately $2.49 thousand.
• You can evaluate on the home screen, graphics screen, or in the table. We choose to use
the home screen, but you should choose the method you prefer.
FINDING A PRODUCT FUNCTION
We illustrate this technique with the functions
given in Example 4 of Section 1.1 of
Calculus Concepts: Milk price = M(x) = 0.02x + 1.90
dollars per gallon on the
xth day of last month and milk sales = S(x) = 1.5 + 0.5(0.8
x
) gallons
of milk sold on the
xth day of last month.
Copyright © Houghton Mifflin Company. All rights reserved.
14

 Loading...
Loading...

















