Texas Instruments TI-84 Plus Guide

TI-83, TI-83 Plus, TI-84 Plus Guide
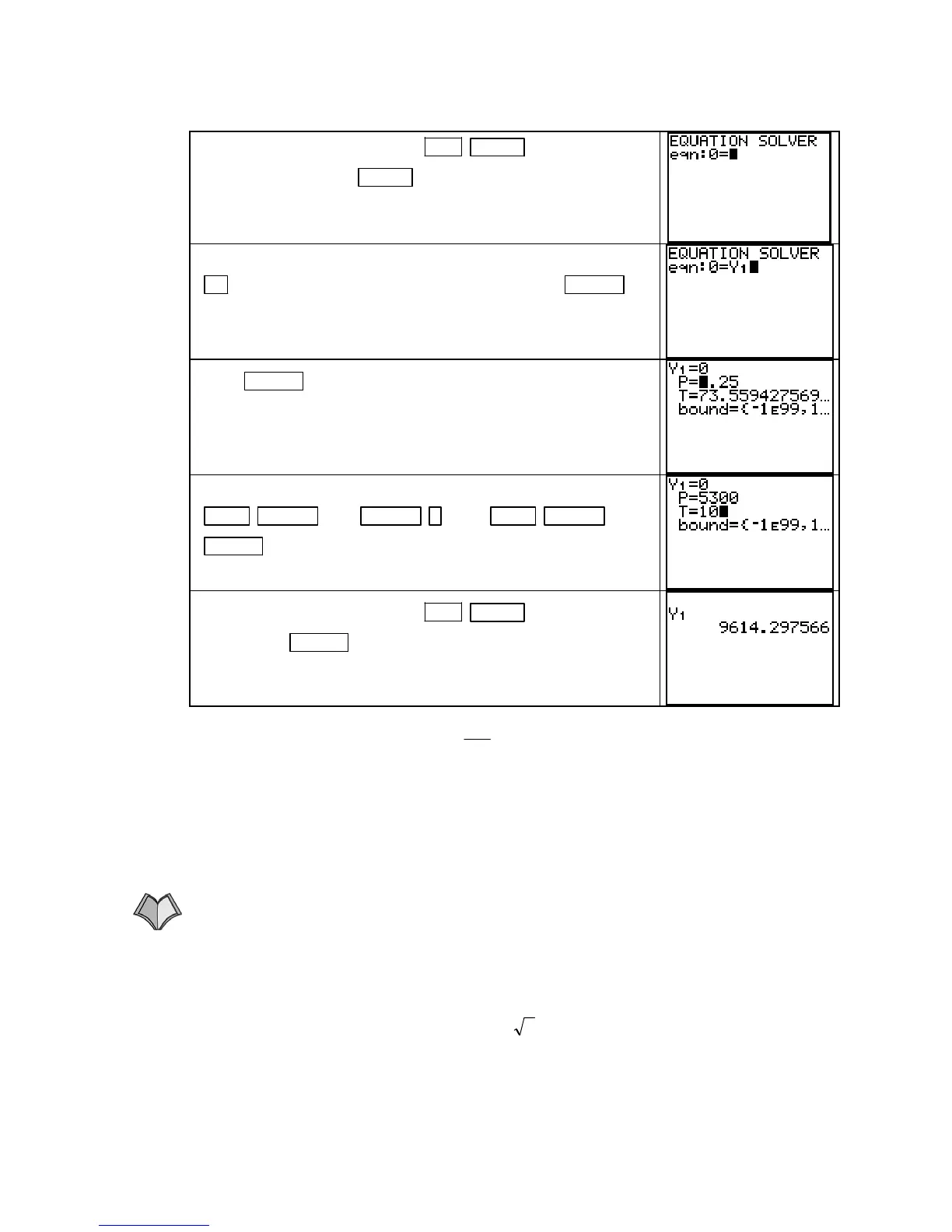
Return to the home screen with
2ND MODE (QUIT). Access
the solver by pressing
MATH 0. If there are no equations
stored in the solver, you will see the screen displayed on the
right.
If you do not see the screen titled EQUATION SOLVER, press
▲ . If the second line does not read eqn:0 = Y1, press CLEAR to
delete the old equation and change so that your screen appears
as shown to the right.
Press ENTER to get the screen shown to the right.
Input the values P = 5300 and t = 10 with the keystrokes 5300
STO
` ALPHA 8 (P) ALPHA . ( : ) 10 STO` ALPHA 4 (T)
ENTER
. This action stores the values P = 5300 and T = 10 in the
calculator.
Return to the home screen with 2ND MODE (QUIT). Type
Y1 and press ENTER
.
To evaluate the function A(P, t) = P 1
006
4
4
+
.
e
t
j
dollars at other values of P and t , return to the
solver and change the stored values. Then go to the home screen and evaluate Y1 again.
CAUTION: It is very important to note at this point that while we have previously used X as
the input variable when entering functions in the
Y= list, we do not follow this rule when we
evaluate functions with more than one input variable. However, realize that we should not
graph
Y1 nor use the TABLE. If you attempt to graph the current Y1 = A(P, t) or use the table,
you will see that the calculator considers this
Y1 a constant. (Check it out and see that the
graph is a horizontal line at about 10467.1 and that all values in the table are about 10467.1.)
9.1.1 SKETCHING CONTOUR CURVES
When given a multivariable function with two input
variables, you can draw contour graphs using the three-step process described below. We illus--
trate with a function that gives body heat loss due to the wind. This function, H, appears in
Example 2 of Section 9.1 of Calculus Concepts:
H(v, t) = (10.45 + 10
v – v)(33 – t) kilogram-calories
per square meter of body surface area per hour for wind speed
v in meters per second.
Step 1: Set H(v, t) = 2000. Because we will use the SOLVER to find the value of t at
various values of
v, write the function as H(v, t) – 2000 = 0.
Copyright © Houghton Mifflin Company. All rights reserved.
97

Texas Instruments TI-84 Plus Specifications

General

Battery type	AAA
Power source	Battery
Number of batteries supported	4
Type	Graphing
Cover	No
Form factor	Pocket
Control type	Buttons
Product color	Black
USB port	Yes
USB 2.0 ports quantity	1
Digits	- digits
Display number of lines	8 lines
Display number of characters	16
RAM capacity	0.024 MB
ROM capacity	0.480 MB
Storage media type	-