TI-83, TI-83 Plus, TI-84 Plus Guide
Input
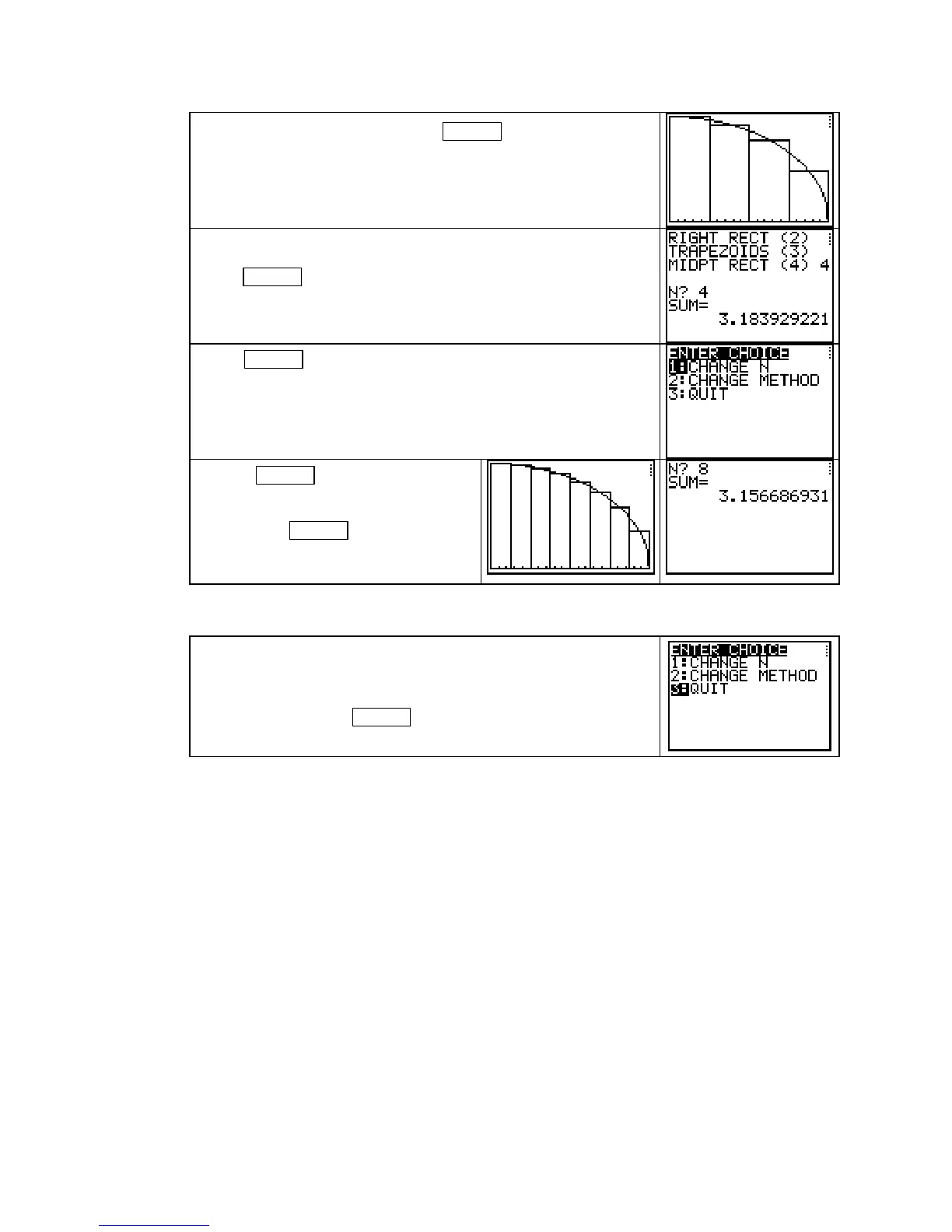
4 at the N? prompt and press ENTER . A graph of the 4
approximating midpoint rectangles and the function are shown.
(Note that the program automatically sets the height of the win-
dow based on the left and right endpoints of the input interval.)
The midpoint-rectangle area is displayed as SUM when you
press
ENTER .
Note: All area approximations are displayed with “SUM.” You need
to remember which method you chose to interpret each result.
Press ENTER once more and some choices are displayed.
Suppose you now want to find the approximating area and see
the figure for 8 midpoint rectangles. Press
1 to change the
method.
Press 8 ENTER at the N? prompt to
view the right rectangles.
Again press
ENTER and the
midpoint-rectangle area estimate is
displayed.
• As you gain more experience with approximation methods using rectangles, you probably
will not want to choose the program option to draw the approximating rectangles.
Continue in this manner and find the left-rectangle area or
change
N and find the left-, right-, or midpoint-rectangle
approximations for different numbers of subintervals.
When finished, press
ENTER and choose 3 to QUIT the
program.
We have seen that using more rectangles results in a more accurate approximation of the
accumulated change. In Example 3 of Section 5.1, the estimate was closer to the actual value
when we used eight rectangles than when we used four rectangles. In Example 4 of Section
5.1, we illustrate the use of increasingly more rectangles to estimate accumulated change. In
this example, you are introduced to a very important and useful concept of calculus -- the
definite integral. Your calculator can be very helpful as you study definite integrals and how
they relate to the accumulation of change.
LIMIT OF SUMS When you are looking for a limit in the midpoint-rectangle approxima-
tions of the area (or signed area) between a function and the horizontal axis between two
values of the input variable, program
NUMINTGL is extremely useful. However, when finding
a limit of sums using the values displayed by this program, it is not advisable to draw pictures
when
N, the number of rectangles, is large.
Copyright © Houghton Mifflin Company. All rights reserved.
71
 Loading...
Loading...

















