Chapter 5
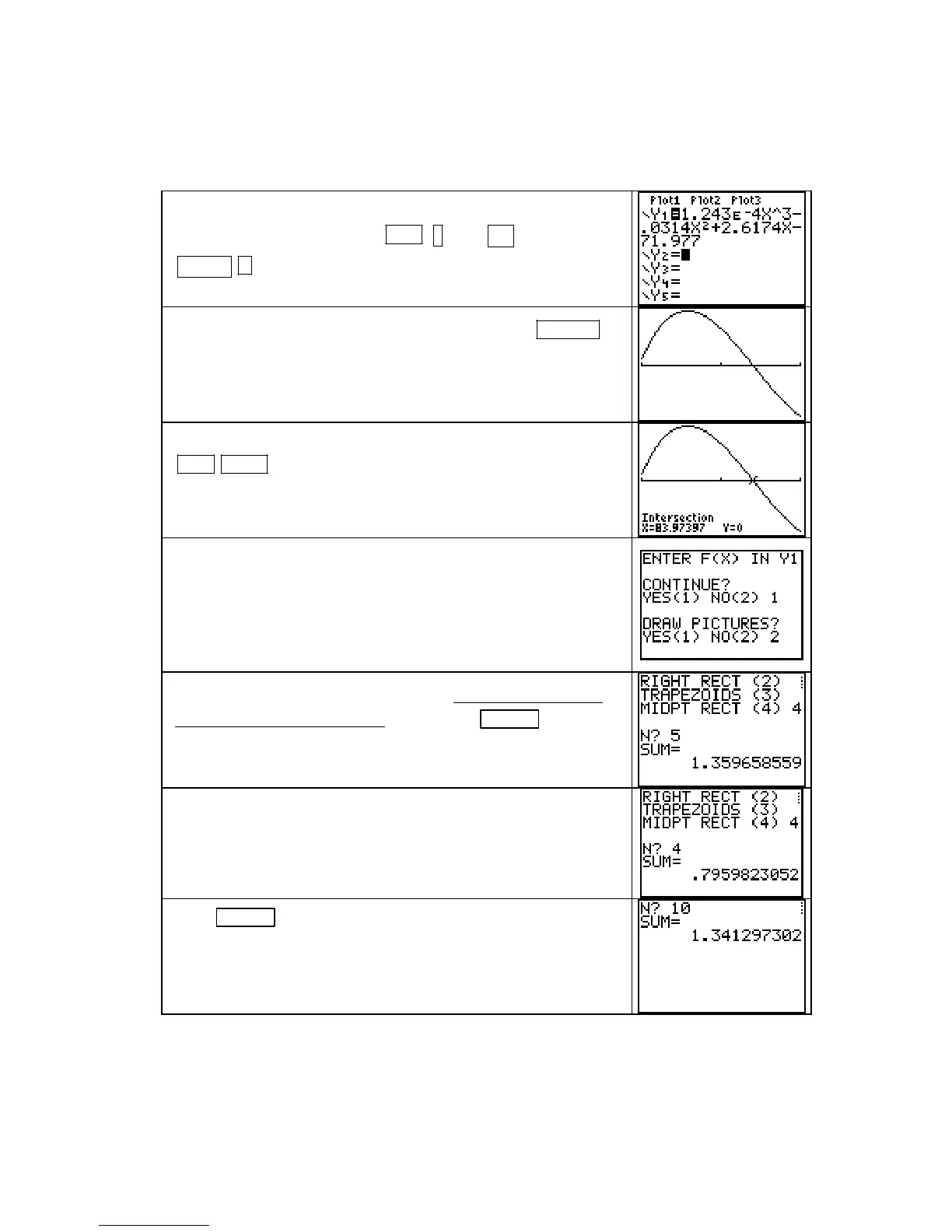
We illustrate using this program to find a limit of sums using W(x) =
(
43 2
1.243 10 0.0314 2.6174 71.977xxx
−
⋅− +−, the function in Example 4 of Section 5.1 of
Calculus Concepts.
Begin by entering the function in Y1. Notice that to enter
(
43
1.243 10
−
⋅ , we used 1.243 2ND , (EE) ()
3
X,T,θ,n ^ 3.
In the window, set Xmin = 70 and Xmax = 90. Use ZOOM 0
(ZoomFit) to graph the equation for the years from 1970 to
1990.
Add the equation Y2 = 0 in the Y = lists. Then use
2ND CALC 5 (intersect) to find the value of the x-intercept
between x = 80 and x = 90.
Run program NUMINTGL. At the first prompt, enter 1 to
continue and enter 2 to not draw pictures.
At the
LEFT ENDPOINT? prompt, enter 70, and at the RIGHT
ENDPOINT?
prompt, enter 83.97397 to tell the calculator that the
input interval is from x = 70 to x = 83.97397. (Use all the
decimals shown for the intersection.)
You are next shown a menu of choices. Always use midpoint
rectangles with a limit of sums. Press 4 and ENTER . At the
N?
prompt, enter 5.
Record on paper the area estimate for 5 midpoint rectangles.
(You should record at least one more decimal place than the
number of places needed for the required accuracy. We record
1.35966 as our approximation.)
Press ENTER to continue the program, and press 1 to choose
CHANGE N. Now double the number of rectangles by entering
N = 10.
(We record 1.34130 as our approximation.)
Copyright © Houghton Mifflin Company. All rights reserved.
72
To Next Page
Loading...
Need help?
General
