Chapter 8
Run the program. Each time the program stops for input or for
you to view a result, press
ENTER to continue.
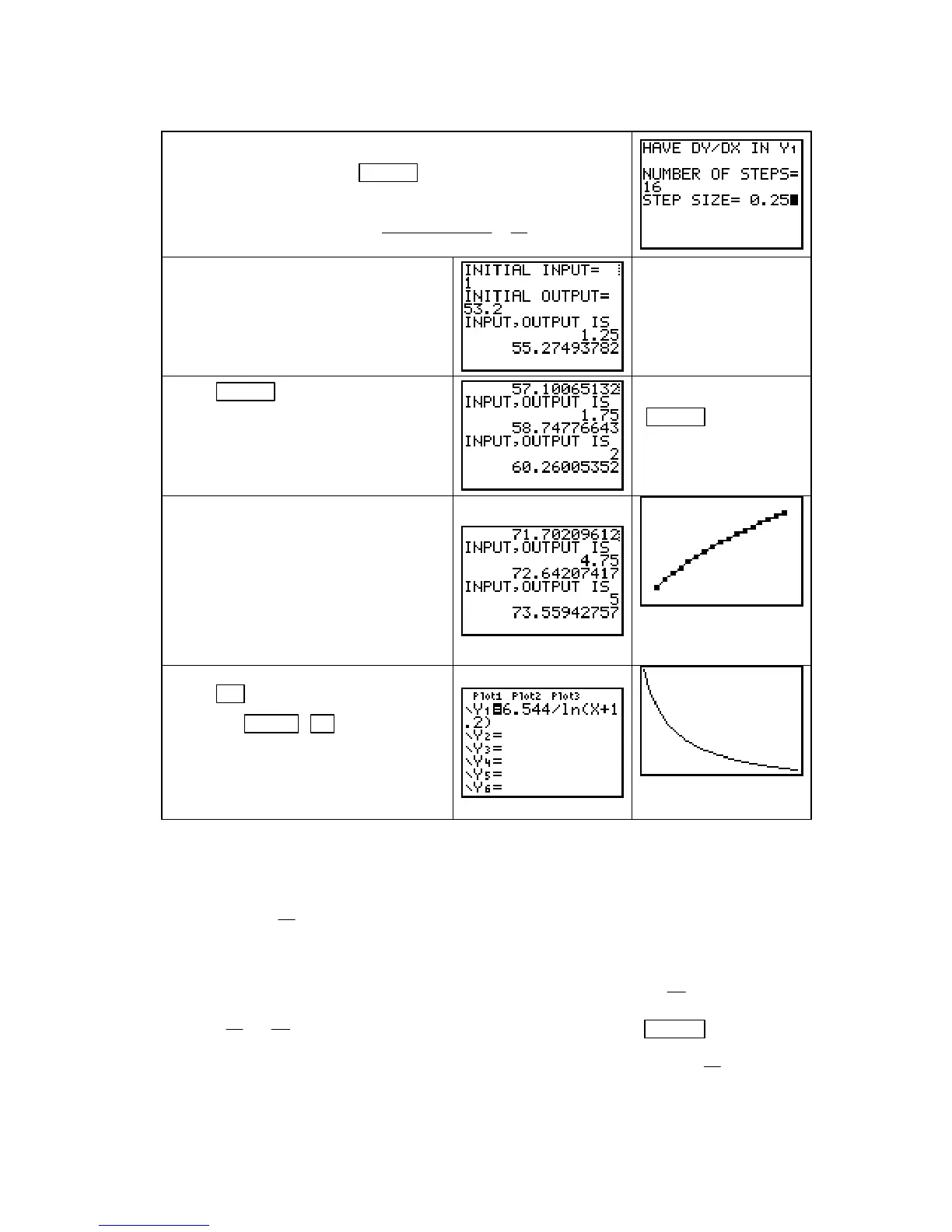
We choose to use 16 steps. Enter this value. The interval is 4
years, so enter the step size =
length of interval
number of steps
=
4
16
= 0.25.
The initial condition is given as the
point (1, 53.2). Enter these values
when prompted for them.
The first application of
the formula gives an
estimate for the value
of the total sales at
x = 1.25:
S(1.25) ≈ 55.275
Press ENTER several more times to
obtain more estimates for total sales.
Record the input values and output
estimates on paper as the program
displays them.
Continue pressing
ENTER to obtain
more estimates of
points on the total
sales function S.
When 16 steps have been completed
(that is, after the input reaches 5), the
program draws a graph of the points
(input, output estimate) connected
with line segments. This solution
graph is an estimate of the graph of
the differential equation solution.
This is an estimate of the
graph of the function
S(t).
Press Y= , turn Plot3 off, turn Y1 on,
and press
ZOOM ▲ [Zoomfit] to
draw the graph of the differential
equation.
This is the slope graph –
the graph of S′(t).
EULER’S METHOD FOR A DIFFERENTIAL EQUATION WITH TWO INPUT
VARIABLES We illustrate the use of Program
EULER with two variables using Example 2
from section 8.3. Follow the same process that is illustrated in the previous section of this
Guide, but enter
dy
dx
in Y1 using the letters x and y as they are written in the given equation.
If the differential equation is written in terms of variables other than x and y, let the deriva-
tive symbol be your guide as to which variable corresponds to the input and which corresponds
to the output. For instance, if the rate of change of a quantity is given by
dP
dn
= 1.346P(1 − n
2
),
compare
dy
dx
to
dP
dn
, entering in Y1 the expression 1.346Y(1 – X
2
). Use ALPHA 1 (Y) to type Y.
dy
dx
The differential equation may be given in terms of y only. For instance, if
= k(30 – y)
where k is a constant, enter
Y1 = K(30 – Y). Of course, you need to store a value for k or substi-
Copyright © Houghton Mifflin Company. All rights reserved.
94

 Loading...
Loading...

















