Chapter 2
2.3 Derivative Notation and Numerical Estimates
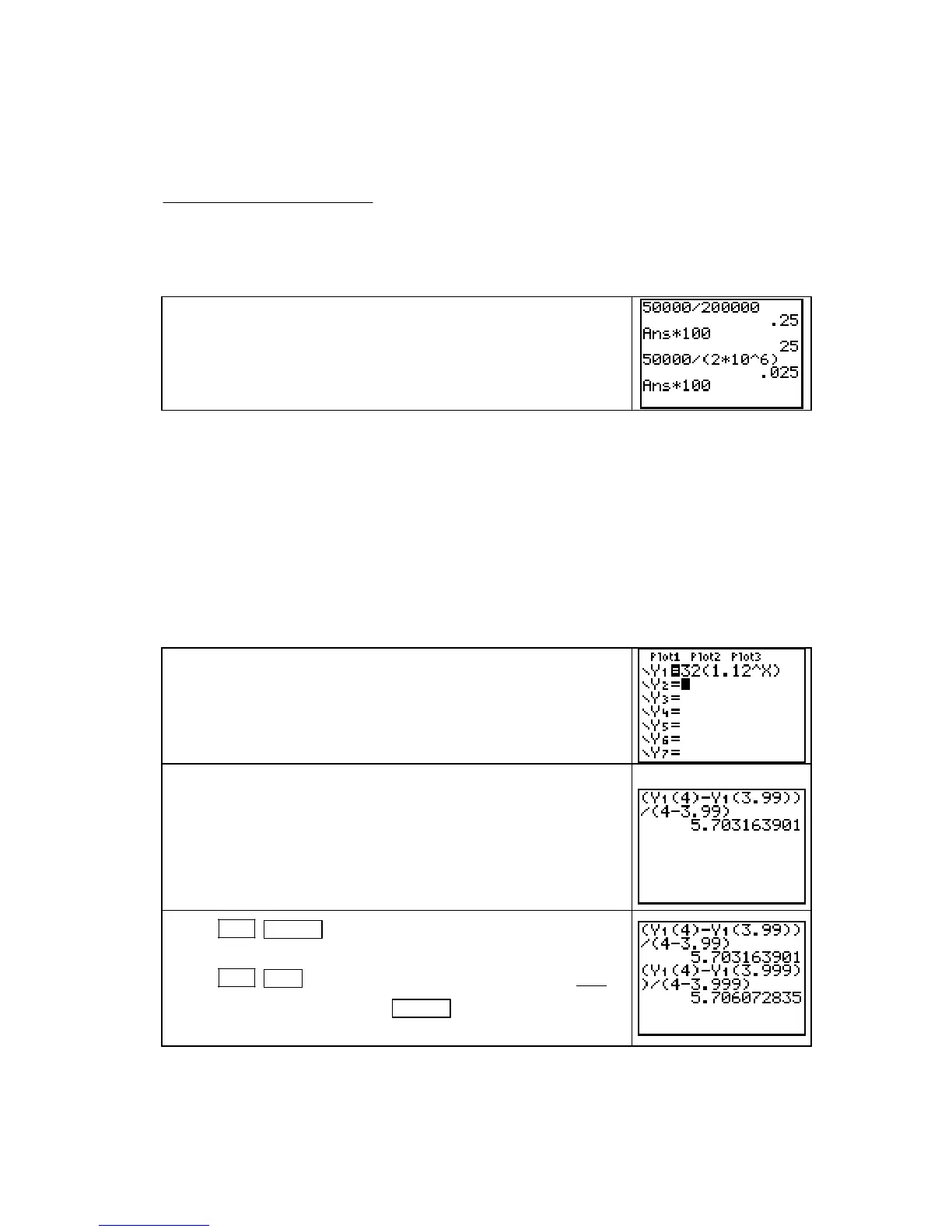
CALCULATING PERCENTAGE RATE OF CHANGE Percentage rate of change =
rate of change at a point
100%
value of the function at that point
⋅
. We illustrate calculating the percentage rate of change
with the example found on page 134 in Section 2.3 of Calculus Concepts. Suppose the
growth rate of a population is 50,000 people per year and the current population size is
200,000 people.
What is the percentage rate of change of the population? The
answer is 25% per year.
Suppose instead that the current population size is 2 million.
What is the percentage rate of change? The answer is 2.5% per
year, which is a much smaller percentage rate of change.
Using your calculator to find slopes of tangent lines does not involve a new procedure. How-
ever, the techniques that are discussed in this section allow you to repeatedly apply a method
of finding slopes that gives quick and accurate results.
NUMERICALLY ESTIMATING A RATE OF CHANGE
Finding the slopes of secant
lines joining the point at which the tangent line is drawn to increasingly close points on a
function to the left and right of the point of tangency is easily done using your calculator. We
illustrate this technique using the function in Example 5 of Section 2.3. Suppose we want to
numerically estimate the slope of the tangent line at t = 5 to the graph of the function that gives
the value of an investment given by: y =
32 1.12
t
billion dollars after t years.
Enter the equation in the Y1 location of the Y= list.
We now evaluate the slopes of secant lines that join close points
to the left of t = 4 with t = 4.
On the home screen, type in the expression shown to the right to
compute the slope of the secant line joining the close point
where t = 3.99 and the point of tangency where t = 4.
Record on paper each slope, to at least 1 more decimal place than
the desired accuracy, as it is computed. You are asked to find
the nearest whole number that these slopes are approaching, so
record at least one decimal place in your table of slopes.
Press 2ND ENTER (ENTRY) to recall the last entry, and then
use the arrow keys to move the cursor over a 9 in the “3.99”.
Press
2ND DEL (INS) and press 9 to insert another 9 in both
places that 3.99 appears. Press
ENTER to find the slope of the
secant line joining t = 3.999 and t = 4.
Copyright © Houghton Mifflin Company. All rights reserved.
50

 Loading...
Loading...

















