TI-83, TI-83 Plus, TI-84 Plus Guide
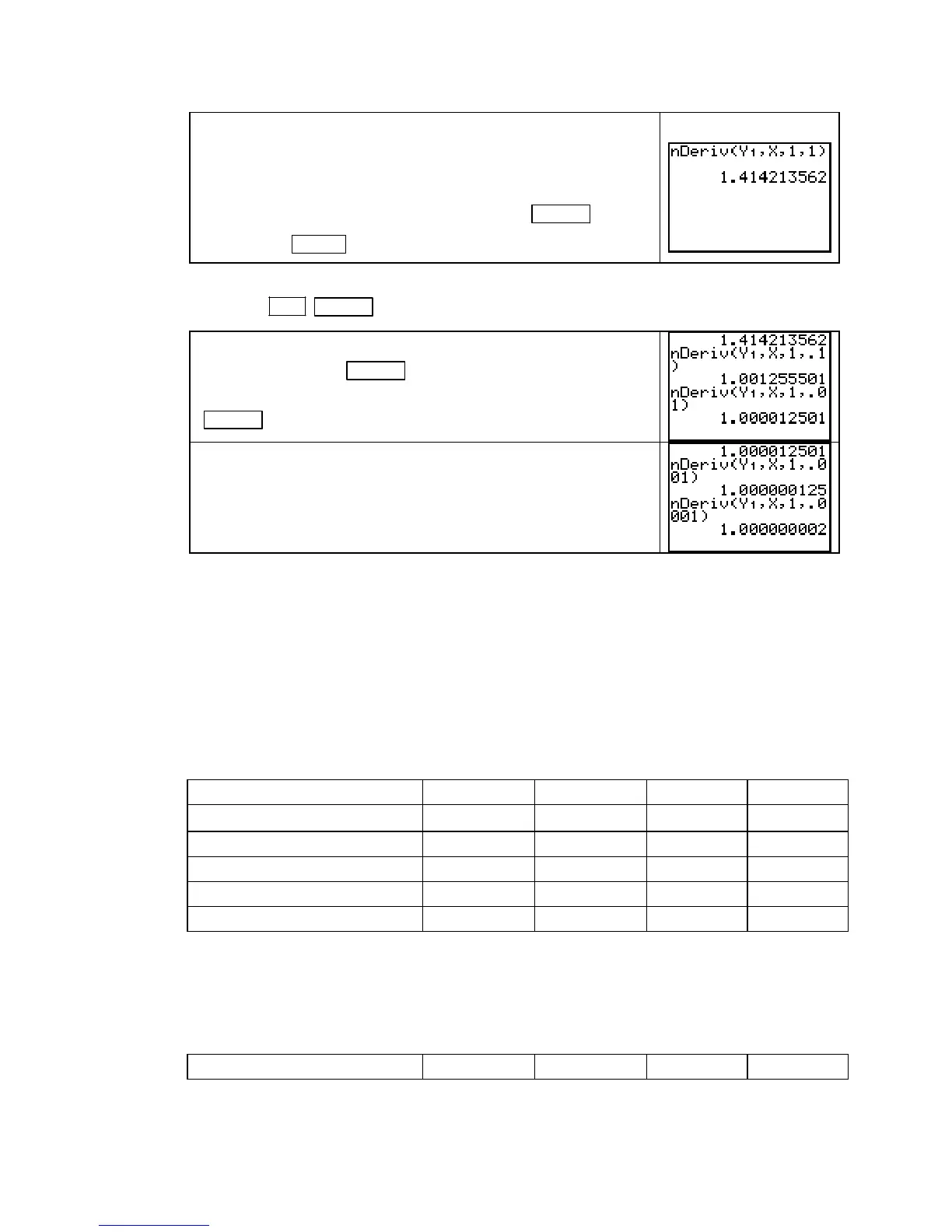
Suppose you want to find the slope of the secant line between
the points (0, f(0)) and (2, f(2)). That is, you are finding the
slope of the secant line between the points (a
−
k, f(a
−
k)) and
(a + k, f(a + k)) for a = 1 and k = 1.
Type the expression on the right and then press
ENTER . Access
nDeriv( with MATH 8 [nDeriv(].
Remember that when you are on the home screen, you can recall previous instructions with the
keystrokes
2ND ENTER (ENTRY).
Recall the last entry and edit the expression so that k changes
from 1 to 0.1. Press
ENTER . Again recall the last entry, and
edit the expression so that k changes from 0.1 to 0.01. Press
ENTER .
Repeat the process for k = 0.001 and k = 0.0001. Note how the
results are changing. As k becomes smaller and smaller, the
secant line slope is becoming closer and closer to 1.
• A logical conclusion is that the tangent line slope is 1. However, realize that we have
just done another type of numerical investigation, not an algebraic proof.
In the table below, the first row lists some values of a, the input of a point of tangency, and
the second row gives the actual slope (to 7 decimal places) of the tangent line at those values.
The algebraic method gives the exact slope of the line tangent to the graph of f at these input
values.
Use your calculator to verify the values in the third through sixth rows that give the slope
of the secant line (to 7 decimal places) between the points (a
−
k, f(a
−
k)) and (a + k, f(a + k))
for the indicated values of k. Find each secant line slope with
nDeriv(Y1, X, a, k).
a = input of point of tangency 2.3
5 12.82 62.7
slope of tangent line = f
′
(a)
0.6593805 0.4472136 0.2792904 0.1262892
slope of secant line, k = 0.1 0.6595364 0.4472360 0.2792925 0.1262892
slope of secant line, k = 0.01 0.6593820 0.4472138 0.2792904 0.1262892
slope of secant line, k = 0.001 0.6593805 0.4472136 0.2792904 0.1262892
slope of secant line, k = 0.0001 0.6593805 0.4472136 0.2792904 0.1262892
You can see that the slope of the secant line is very close to the slope of the tangent line for
small values of k. For this function, the slope of the secant line does a great job of approxi-
mating the slope of the tangent line when k is very small.
Now repeat the process, but do not include k in the instruction. That is, find the secant line
slope by calculating
nDeriv(Y1, X, a, k). Did you obtain the following (to 7 decimal places)?
slope of secant line 0.6593805 0.4472136 0.2792904 0.1262892
Copyright © Houghton Mifflin Company. All rights reserved.
53

 Loading...
Loading...

















