Chapter 2
In this section, we investigate what the calculator does if you ask it to draw a tangent line
where the line cannot be drawn. Consider these special cases:
1. What happens if the tangent line is vertical? We consider the function f(x) = (x + 1)
1/3
which has a vertical tangent at x =
–
1.
2. How does the calculator respond when the instantaneous rate of change at a point does not
exist? We illustrate with g(x) = |x| – 1, a function that has a sharp point at (0,
−
1).
3. Does the calculator draw the tangent line at the break point(s) of a piecewise continuous
function? We consider two situations:
a. y = h(x), a piecewise continuous function that is continuous at all points, and
b. y = m(x), a piecewise continuous function that is not continuous at x = 1.
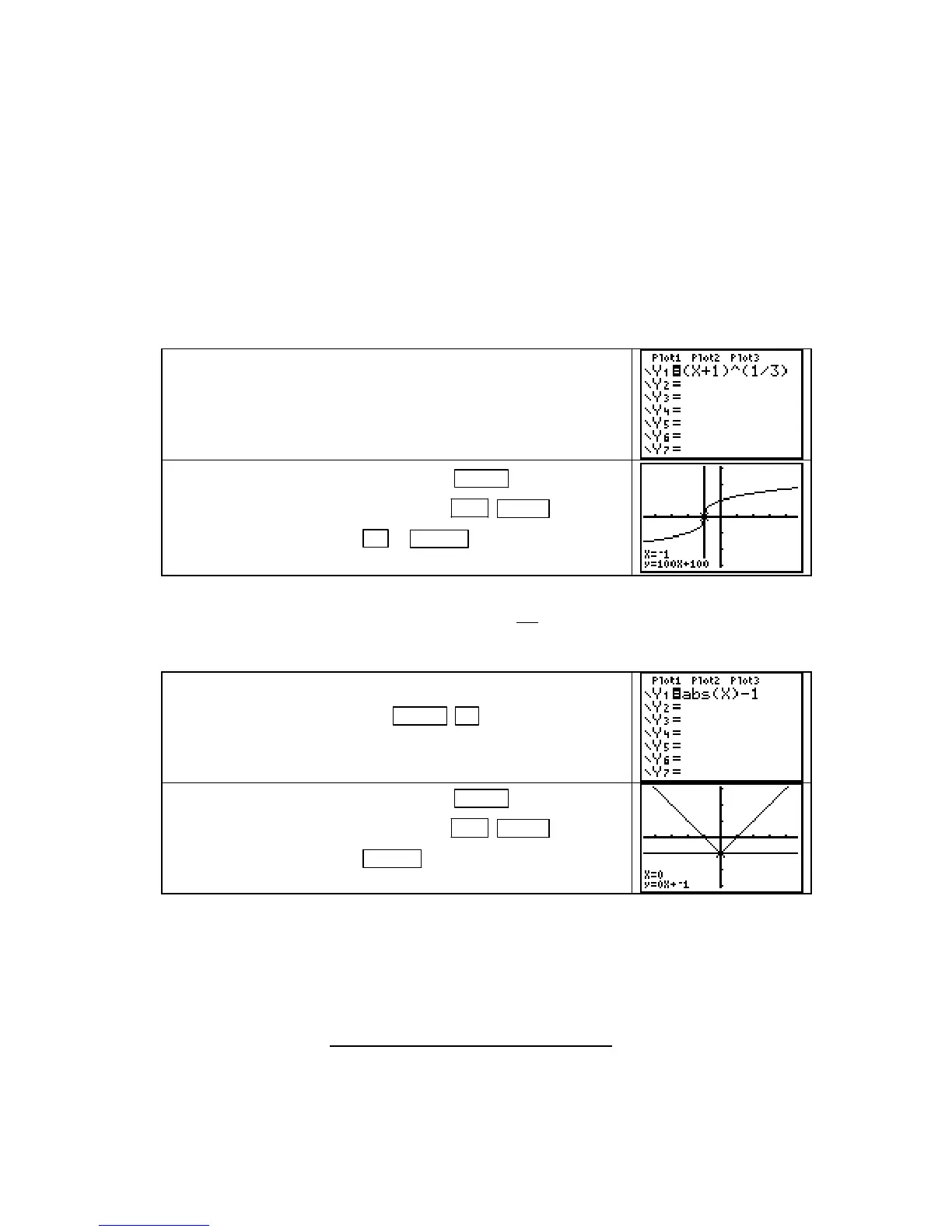
1. Enter the function f(x) = (x + 1)
1/3
in the Y1 location of the
Y= list. Remember that anytime there is more than one
symbol in an exponent and you are not sure of the
calculator’s order of operations, enclose the power in
parentheses.
Draw the graph of the function with ZOOM 4 [ZDecimal].
With the graph on the screen, press
2ND PRGM (DRAW)
5 [Tangent(],
then press (−) 1 ENTER . The tangent line is
drawn at
x =
−
1.
CAUTION: Note that the calculator correctly draws the vertical tangent. However, the
equation of the vertical tangent line is x =
−
1, not y = 100x + 100. The line whose equa-
tion is printed on the calculator screen has slope 100, but the instantaneous rate of
change at (
−
1, 0) does not exist because the tangent is vertical.
2. Clear Y1 and enter the function g(x) = |x| – 1. The absolute
value symbol is typed with
MATH ► 1 [abs(].
Draw the graph of the function with ZOOM 4 [ZDecimal].
With the graph on the screen, press 2ND PRGM (DRAW)
5 [Tangent(],
then press ENTER . The tangent line is drawn
at
x = 0.
THIS IS INCORRECT. There is a sharp point on the graph of g at (0,
–
1), and the
limiting positions of secant lines from the left and the right at that point are different. A
tangent line cannot be drawn on the graph of g at (0,
–
1) according to our definition of
instantaneous rate of change. The calculator’s definition is different, and this is why the
line is drawn. (The calculator’s definition is explained in on page A-48 of this Guide.)
CAUTION: Note that the calculator gives the correct equation for the line that is
drawn. However,
there is no tangent line at this sharp point on this continuous function.
Copyright © Houghton Mifflin Company. All rights reserved.
48

 Loading...
Loading...

















