Vigor VS Series User Manual

(7) Floating Point (Real number)
41
The PLC was provided with Floating Point instructions therefore the PLC can calculate decimal numbers.
The decimal numbers are storage and calculated in a PLC using two different pattern formats: Binary Floating Point
Number and Decimal Floating Point Number. The expositions are showed below.
D1( b15〜 b0)
S E7
E6
E1
E0
A22 A21
A16 A15
A14 A1
A0
7
2
6
2
1
2
0
2
-1
2
-2
2
-7
2
-8
2
-9
2
-22
2
-23
2
D0( b15〜 b0)
(D1,D0)
b31 b30 b29 b24 b23 b22 b21 b16 b15 b14 b1 b0
D3
D2
(D3,D2)
b15 b14 b13 b2 b1 b0 b15 b14 b13 b2
b1 b0
In the PLC program, the real constant value is usually preceded by the “E”. The effective range of real
38 38
constants is -3.402×10 ~ 3.402×10 , which can be expressed by the decimal point or exponent.
By the decimal point: Directly use decimal point to express the value, for example, “E102.35” represents
“102.35”.
By the exponent: Use the mathematical exponent to express, for example, “E1.0235+2” represents “102.35”;
+2
“+2” means to multiply by 10 .
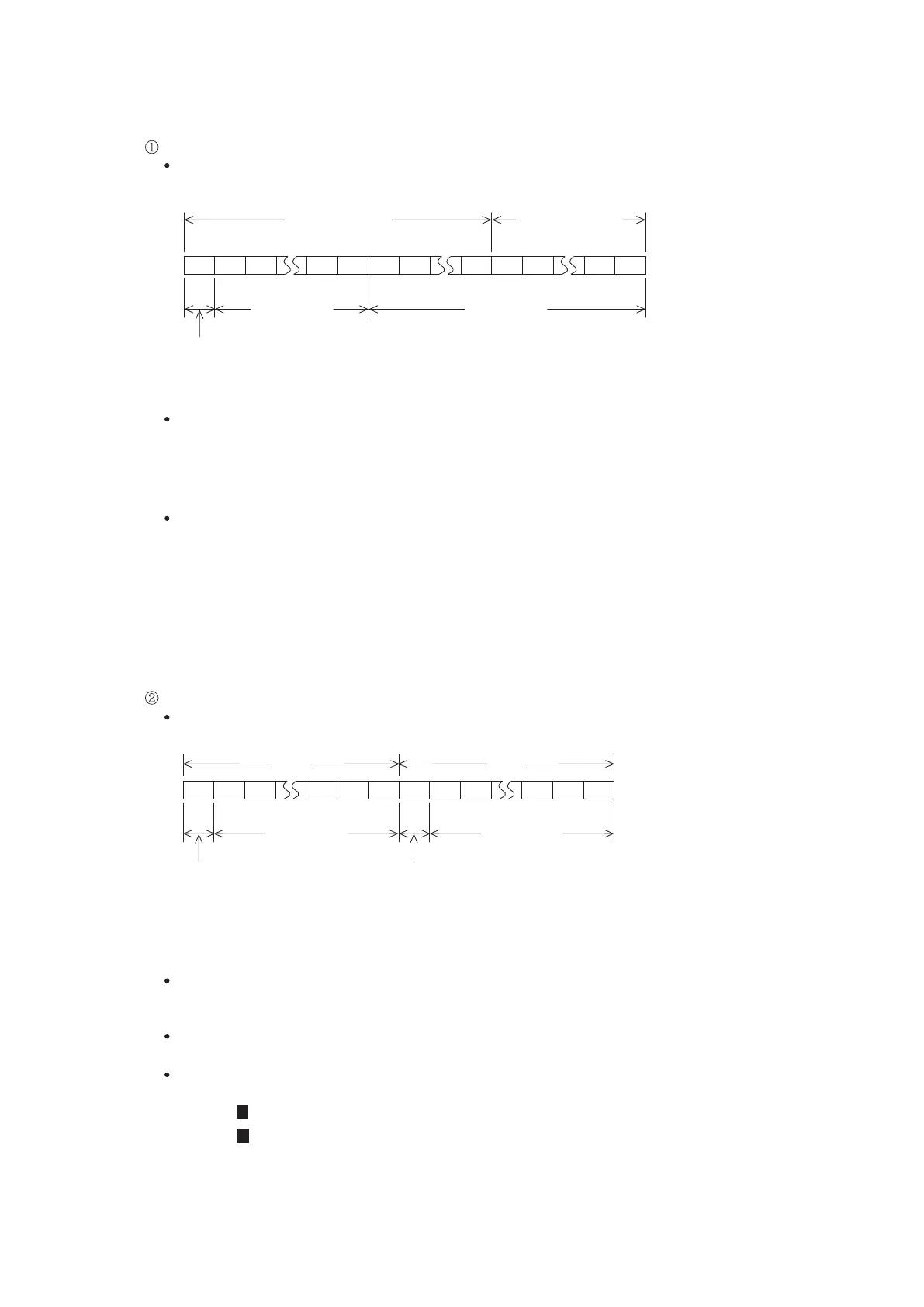
Binary Floating Point Number
Inside of the PLC, the Floating Point calculates and decimal number storages are using Binary Floating Point
Numbers. A Binary Floating Point Number's value storage format is composed of 2 sequential registers. It is
an example, using (D1,D0) to explain a format of a Binary Floating Point Number.
Exponent
(8 bits)
Mantissa
(23 bits)
Mantissa Sing bit (1=Negative, 0=Positive)
Binary Floating Point Number's value
7 6 1 0
0 -1 -2 -22 -23 (E7×2 +E6×2 +.....+E1×2 ＋ E0×2 ) 127
=±(2 +A22×2 +A21×2 +.....+A1×2 +A0×2 )×2 /2
If S=0, A22=1, A21=1, A20~A0=0
E7=1, E6~E0=0
Therefor, the Binary Floating Point Number's value storage in the register (D1,D0) is equal to
7 6 0
0 -1 -2 -23 (1×2 +0×2 +.....+0×2 ) 127
(2 +1×2 +1×2 +.....+0×2 )×2 /2
128 127 1
=1.75×2 /2 =1.75×2
A Binary Floating Point Number’s value limit:
128 -126 -126 128
−1.0 × 2 ~ −1.0 × 2 , 0, 1.0 × 2 ~ 1.0 × 2
38
Maximum modulus: 3.402×10
Exponent
(16 bits)
Mantissa
(16 bits)
Exponent Sing bit
(1=Negative, 0=Positive) MSB
Mantissa Sing bit
(1=Negative, 0=Positive) MSB
Decimal Floating Point Number
A Decimal Floating Point Number’s value storage format is also composed of 2 sequential registers. It is an
example, using (D3,D2) to explain a format of a Decimal Floating Point Number.
(Exponent)
Decimal Floating Point Number’s value= (Mantissa) ×10
Mantissa =±(1000 ~ 9999) Exponent= -41 ~ +35
If D2=1234, D3=-1
A Decimal Floating Point Number’s value limit:
-41 35
Minimum modulus: 1175×10 Maximum modulus: 3402×10
The Binary Floating Point Number and Decimal Floating Point Number can use the instructions to convert the
value:
FNC118 ( EBCD ): To convert from a Binary Floating Point Number to a Decimal Floating Point Number.D
FNC119 ( EBIN ): To convert from a Decimal Floating Point Number to a Binary Floating Point Number.D
Therefor, the Decimal Floating Point Number’s value storage in the register (D3,D2) is equal to
-1
1234×10 ＝123.4
-38
Minimum modulus: 1.175×10

Vigor VS Series Specifications

General

Brand	Vigor
Model	VS Series
Category	Controller
Language	English