Lorrca MaxSis - Page 206

Appendix for Lorrca® MaxSis
Page 204 Lorrca Maxsis User Manual
Version 5.04 MRN-231-EN
The distance of a data point to the obtained ellipse has to be calculated in order to reject outliers.
Calculating this distance requires solving a quadratic equation, which is an inefficient procedure. A
good approximation can be obtained using orthogonal hyperbola. (References 50
12
, 51
13
) Confocal
ellipses and hyperbola intersect orthogonally (see Figure 4 section b). This property is exploited to
find the confocal hyperbola that crosses a specific data point. The distance from the data point to
the point of intersection between the ellipse and the hyperbola provides a good approximation of
the shortest distance to the ellipse. (References 50
14
, 51
15
) The average distance of the edge
pixels to the best-fit ellipse is defined as the Error Of Fit (Eof) parameter.
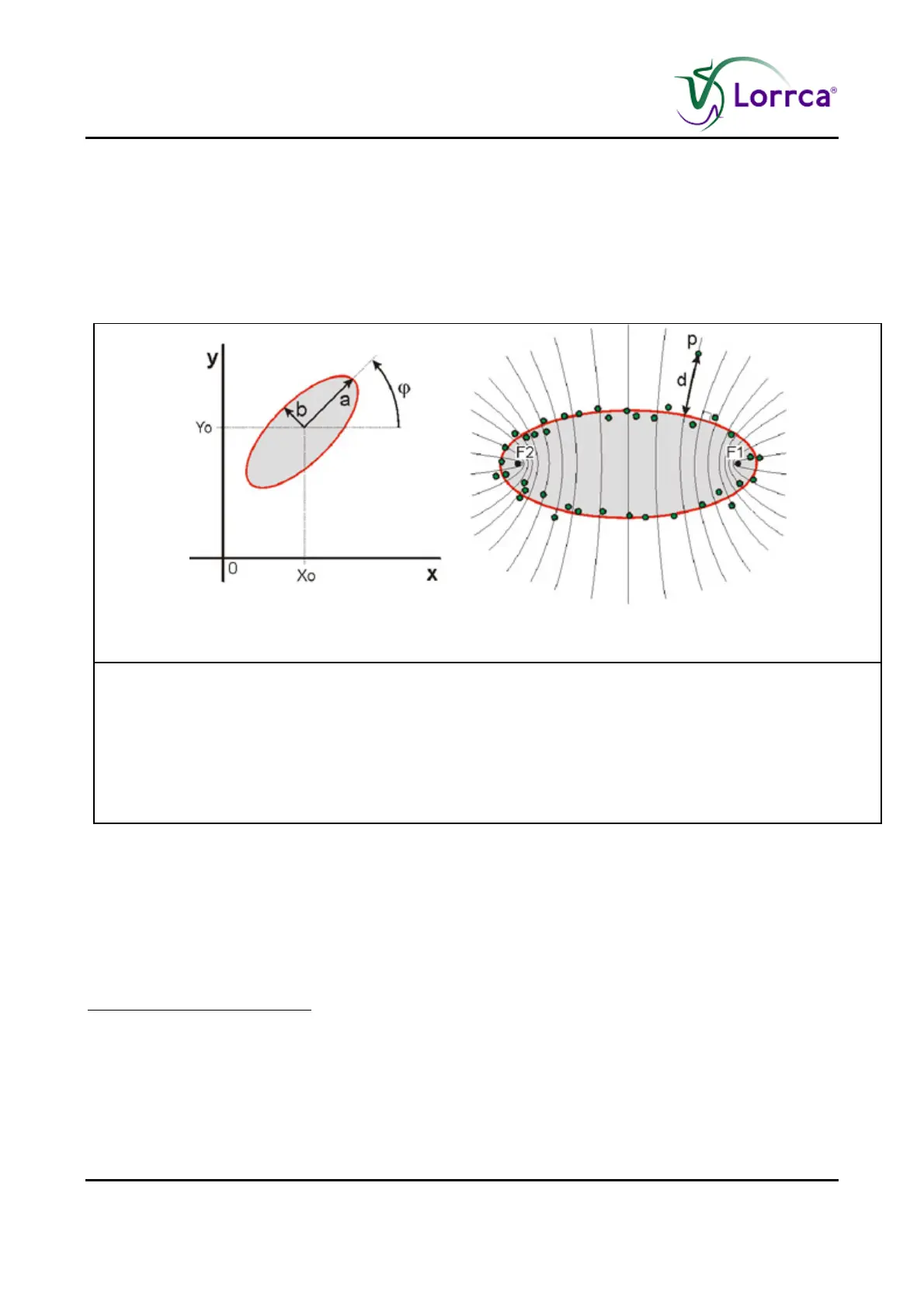
Figure 4: Tilted ellipse with its five ellipse parameters
Figure 4.
A. Tilted ellipse with its five ellipse parameters indicated: location (x
0
,
y
0
), orientation () and axes (a,b),
B. the closest distance of a data point to the best-fit ellipse is estimated
using the confocal hyperbola that goes through the data points and
intersects the ellipse orthogonally.
Accuracy of ellipse parameters.
The accuracy of the ellipse parameters is determined in one of two possible ways.
1. If one configures the software to analyse a certain number of diffraction patterns in order to
reduce measurement inaccuracy, the programs displays the mean and standard deviation for
each of the obtained ellipse parameters, and of the derived parameters (such as the EI).
12
Rosin P.L., Ellipse fitting using orthogonal hyperbolae and Stirling's oval, Graphical Models and Image
Processing, vol. 60:(3), pp. 209-213, May 1998.
13
Rosin P.L., Analysing error of fit functions for ellipses, Pattern Recognit. Lett., vol. 17, pp. 1461-1470,
1996.
14
Rosin P.L., Ellipse fitting using orthogonal hyperbolae and Stirling's oval, Graphical Models and Image
Processing, vol. 60:(3), pp. 209-213, May 1998.
15
Rosin P.L., Analysing error of fit functions for ellipses, Pattern Recognit. Lett., vol. 17, pp. 1461-1470,
1996.