Appendix for Lorrca® MaxSis
Page 208 Lorrca Maxsis User Manual
Version 5.04 MRN-231-EN
11.6.2.2.2. Tri-exponential syllectogram representation
The conventional mathematical representation of the syllectogram contains two time-constants and
describes the curve from the peak onward. (References 6
23
, 23
24
, 31
25
) The tri-exponential
representation (References 15
26
, 16
27
) introduces a third time-constant to include the upstroke
caused by RBC shape recovery. (Reference 5
28
) Thus, the intensity curve I(t) was fitted using a tri-
exponential function containing three time-constants associated with RBC-shape recovery (T
r
),
rouleaux formation (T
f
) and 3D aggregate formation (T
s
):
(Equation 4)
where I
r
, I
f
, and Is denote the contribution of shape recovery, (fast) rouleaux formation and (slow)
3D aggregate formation, respectively.
The curve fit is performed using the Levenberg-Marquardt algorithm (Reference 46
29
) for fitting
non-linear functions. Since the syllectogram is sampled uniformly most data points stem from the
tail of the curve. To prevent the fitting algorithm from focusing on this region, the curves were re-
sampled by selecting 300 points uniformly distributed on a logarithmic time scale.
Several aggregation parameters are derived from the syllectogram as indicated in Figure 6. To be
able to distinguish “fitted” intensity parameters from “conventional” parameters (not resulting from
the curve fit), the latter gives the symbol Isc.
23
Bauersachs R.M., Wenby R.B., Meiselman H.J., Determination of specific red blood cell aggregation
indices via an automated system, Clin. Hemorheol., vol. 9, pp. 1-25, 1989.
24
Firsov N.N., Bjelle A., Korotaeva T.V., Priezzhev A.V., Ryaboshapka O.M., Clinical application of the
measurement of spontaneous erythrocyte aggregation and disaggregation. A pilot study, Clin. Hemorheol.
Microcirc., vol. 18, pp. 87-97, 1998.
25
Hardeman M.R., Goedhart P.T., Dobbe J.G.G., Lettinga K.P., Laser-assisted Optical Rotational Cell
Analyser (LORCA); A new instrument for measurement of various structural hemorheological parameters,
Clin. Hemorheol., vol. 14:(4), pp. 605-618, 1994.
26
Dobbe J.G.G., Engineering developments in hemorheology, PhD Thesis, University of Amsterdam, Sept.
2002.
27
Dobbe J.G.G., Streekstra G.J., Strackee J., Rutten M.C.M., Stijnen J.M.A., Grimbergen C.A.,
Syllectometry: Effect of aggregometer geometry in the assessment of red blood-cell shape recovery and
aggregation, IEEE-Transactions on Biomedical Engineering, vol. 50:(1), pp. 97-106, 2003.
28
Baskurt O.K., Meiselman H.J., Determination of red blood cell shape recovery time constant in a couette
system by the analysis of light reflectance and ektacytometry, Biorheology, vol. 33:(6), pp. 489-503, 1996.
29
Press W.H., Teukolsky A.A., Vetterling W.T., Flannery B.P., Levenberg-Marquardt method, in: Numercal
recipes in C, The art of scientific computing, Cambridge University Press, 2nd ed., pp. 683-688, 1992 (ISBN:
0-521-43108-5).
To Next Page
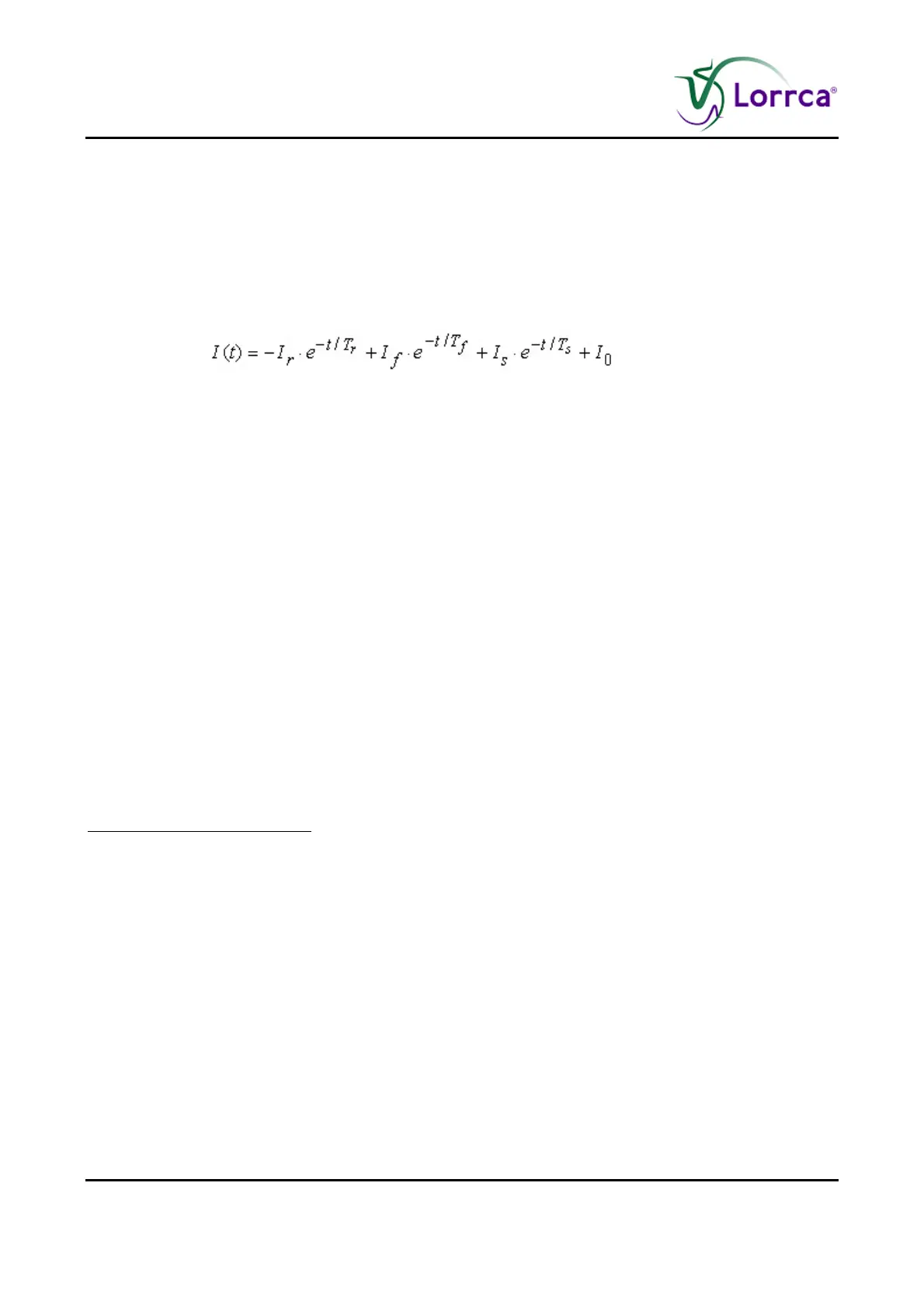Loading...