Library of Function Blocks
4.31
Integral action is transformed into a series of pulses of minimum width AWPL, with a frequency
determined by the integral time T
R
and by the control deviation.
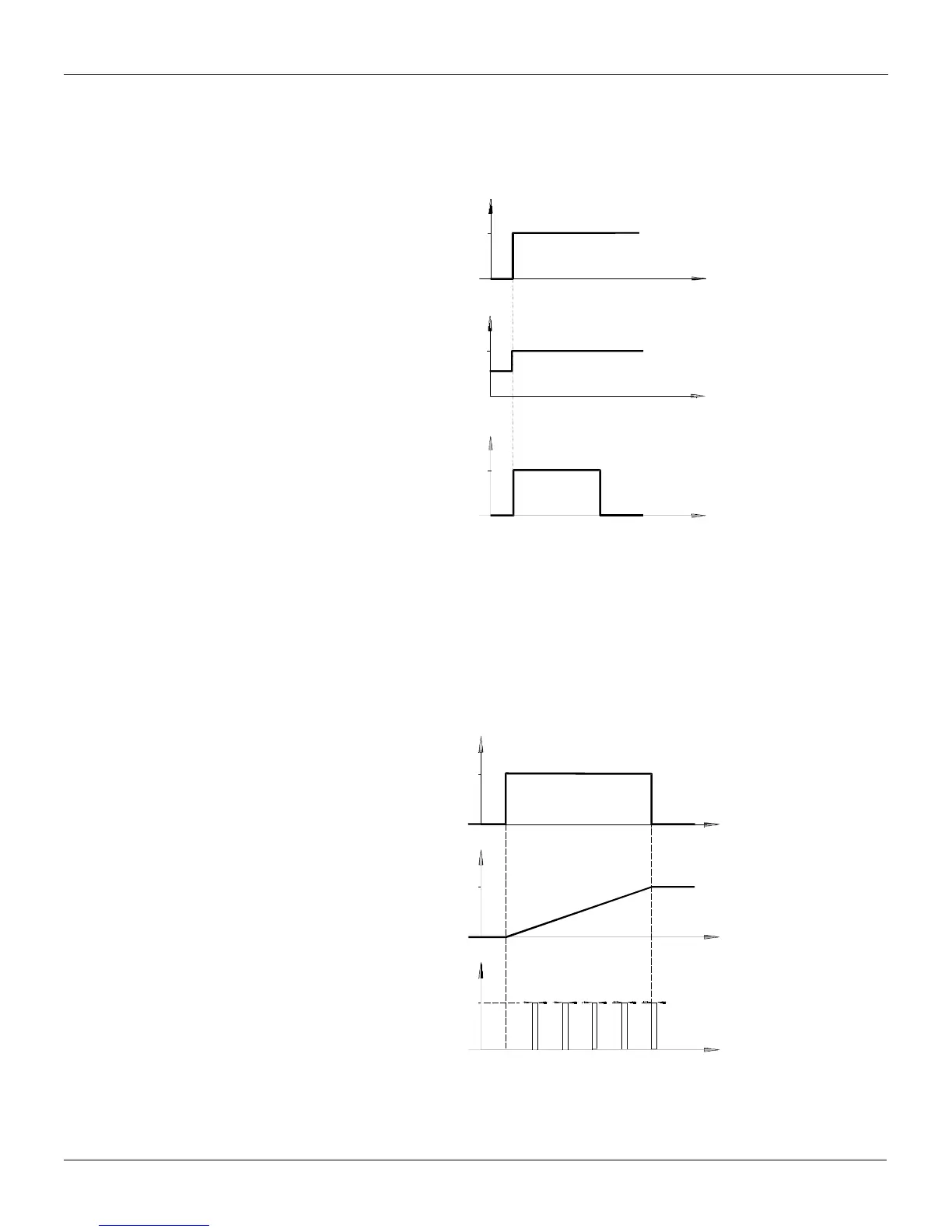
For example, consider a case where the PID is adjusted with proportional gain equal to 1, with no
integral or derivative action; valve opening time = 1 minute and on instant t=0 there is a step error
equal to 25% (Figure 4.11.2).
25%
PID-OUT
75%
50%
STEP-OUT
“ON”
1
e
0
15
0
0
t(sec)
t(sec)
t(sec)
Proportional action
Fig 4.11.2 - Step Output for a 25% deviation with Proportional action only
In this example, 15 seconds of actuation are equivalent to 25% of the valve's excursion (0.25 min =
15 s).
The integral action works as a train of pulses with the same width. The total number of pulses in a
given interval of time depends on the integral action adjustment in the PID and on the individual
width of each pulse (AWPL).
Let's consider a case similar to the above example, where the PID has the integral action adjusted
to 1 minute/repetition and each pulse has a width of 3 seconds. As AWPL is expressed in number of
cycles and each cycle is 0.2 s, AWPL=3/0.2 = 15.
e
PID-OUT
STEP-OUT
25%
25%
“ON” 1
T (sec)
T (sec)
T (sec)
Integral
action only
3
0
060
333 3
Fig 4.11.3 - Step Output for a 25% deviation with Integral action only
The error is 25%. A standard I controller would increase/decrease the output by 25% in 1 minute
(T
R
).
 Loading...
Loading...