YASKAWA NX100 Instructions

8.4 ARM Control
8-42
<Example 3>
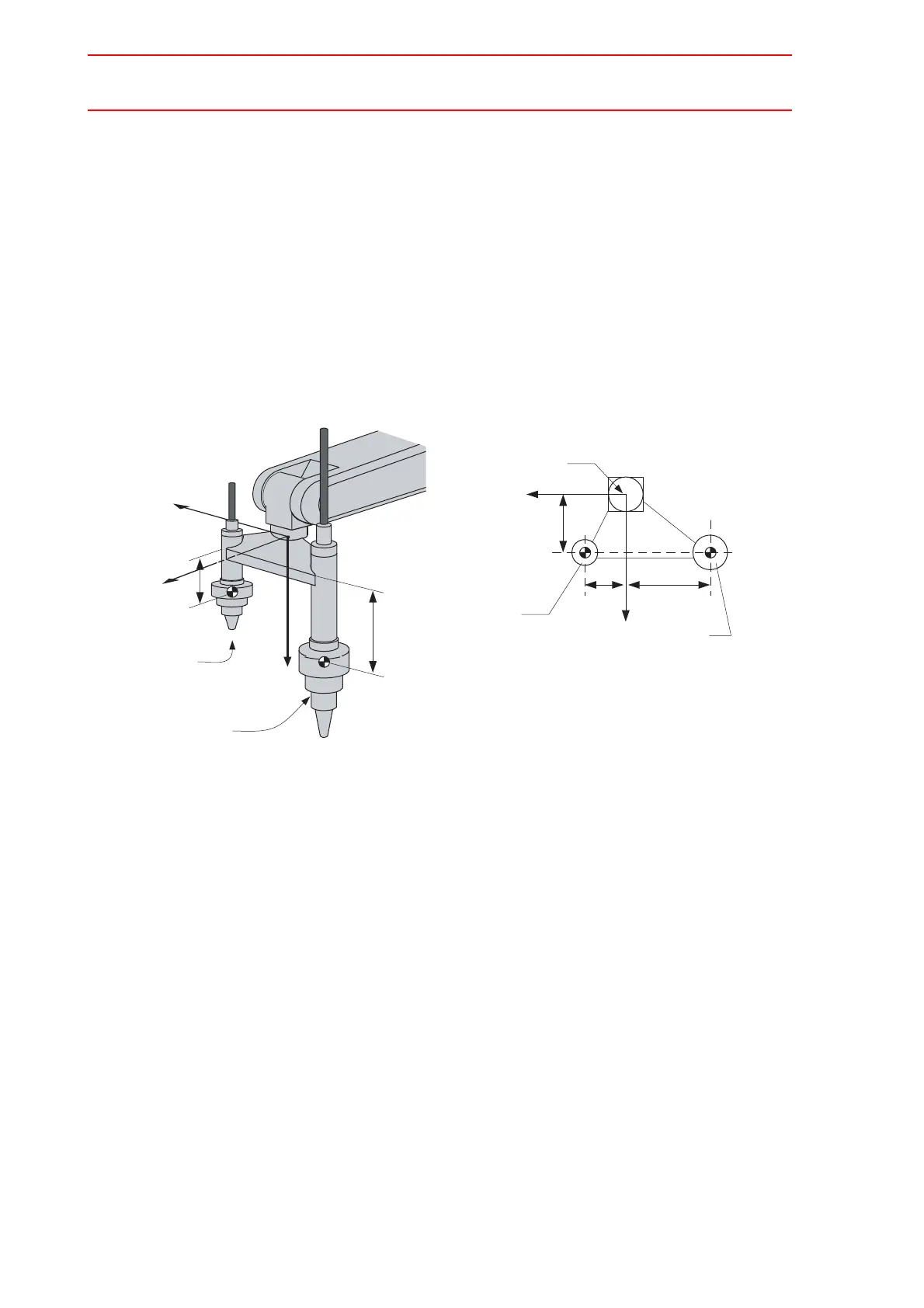
When there are two or more big mass such as the twin gun system as shown in the figure
below, perform:
1. Set the center of gravity position when the center of gravity position of the entire tool is
roughly understood, and set the moment of inertia at the center of gravity calculated by
approximating the entire tool in the shape of hexahedron or cylinder. (It is enough in
this setting usually.); or
2. When weight in each mass and the center of gravity position are understood, the cen-
ter of gravity position and the moment of inertia at the center of gravity of the entire tool
can be calculated. (Refer to forementioned supplement column: "How to calculate
"Center of gravity position" and "moment of inertia at the center of gravity" for plural
mass".)
This example shows the calculation with the method 2.
Weight : W = w1 + w2
= 3 + 6 = 9 = approx. 10[kg]
Center of gravity Xg = (w1 * x1 + w2 * x2) / (w1 + w2)
= (3 * 100 + 6 * 100) / (3+6) = 100.0 [mm]
Yg = (3 * 50 + 6 * (-150)) / (3+6) = -83.333 [mm]
Zg = (3 * 40 + 6 * 70) / (3+6) = 60.0 [mm]
The moment of inertia at the center of gravity position:
Ix =
{ w1 * ((y1 - Yg)
2
+ (z1 - Zg)
2
) * 10
-6
+ Icx1}
+ { w2 * ((y2 - Yg)
2
+ (z2 - Zg)
2
) * 10
-6
+ Icx2}
= 3 * ((50 - (-83))
2
+ (40 - 60)
2
) * 10
-6
+
6 * (((-150) - (-83))
2
+ (70 - 60)
2
) * 10
-6
= 0.082 = approx. 0.100
Iy = 3 * ((100 - 100)
2
+ (40 - 60)
2
) * 10
-6
+ 6 * ((100 - 100)
2
+ (70 - 60)
2
) * 10
-6
= 0.002 = approx. 0.010
Iz = 3 * ((100 - 100)
2
+ (50 - (-83))
2
) * 10
-6
+ 6 * ((100 - 100)
2
+ ((-150) - (-83))
2
) * 10
-6
= 0.080 = approx. 0.100
Y
F
40
70
Gun 1
Gun 2
X
F
Z
F
(Gun 1)
Weight: w1 = 3 kg
Center of Gravity:
x1 = 100 mm
y1 = 50 mm
z1 = 40 mm
(Gun 2)
Weight: w2 = 6 kg
Center of Gravity:
x2 = 100 mm
y2 = -150 mm
z2 = 70 mm
Y
F
X
F
Center of Flange
100
50 150
Gun 1
Gun 2
(Top View)

YASKAWA NX100 Specifications

General

Manufacturer	YASKAWA
Model	NX100
Operating Temperature	0 to 45°C
Humidity	20 to 80% RH (non-condensing)
Communication Interfaces	Ethernet
Safety Standards	ISO 10218-1
Power Supply	200-230V AC, 50/60Hz
Storage Temperature	60°C