Stober PK - Page 182

× × + + × ×
=
× + + ×
3 3
2m,1* 1* 2rad,acc,1* 2m,n* n* 2rad,acc,n*
3
2rad,eq*
2m,1* 1* 2m,n* n*
n t F ... n t F
F
n t ... n t
6.6.2.2 A and S shaft design
Permitted shaft loads for A shaft design (hollow shaft with keyway)
Type z
2
F
2ax20
F
2rad20
F
2rad,acc
M
2k20
M
2k,acc
[mm] [N] [N] [N] [Nm] [Nm]
F1 30.0 900 4200 4200 175 175
F2 33.0 1200 5400 5400 250 250
F3 33.0 1350 7500 7500 375 375
F4 39.0 1900 9250 9250 550 550
F6 45.0 2200 12500 12500 800 800
Permitted shaft loads for S shaft design (hollow shaft with shrink ring)
Type z
2
F
2ax20
F
2rad20
F
2rad,acc
M
2k20
M
2k,acc
[mm] [N] [N] [N] [Nm] [Nm]
F1 30.0 900 4200 4200 175 175
F2 33.0 1200 5400 5400 250 250
F3 33.0 1350 7500 7500 375 375
F4 39.0 1900 9250 9250 550 550
F6 45.0 2200 12500 12500 800 800
For other output speeds, download diagrams at https://configurator.stoeber.de/en-US/
.
The following applies to output speeds n
2m*
> 20 rpm:
2ax 20
2axN
2m*
3
1
F
F
n
20min
-
=
rpm
2rad20
2radN
2m*
3
1
F
F
n
20min
-
=
rpm
2k 20
2kN
2m*
3
1
M
M
n
20min
-
=
rpm
The values for F
2ax20
, F
2rad20
and M
2k20
can be found in the table "Permitted shaft loads" in this chapter.
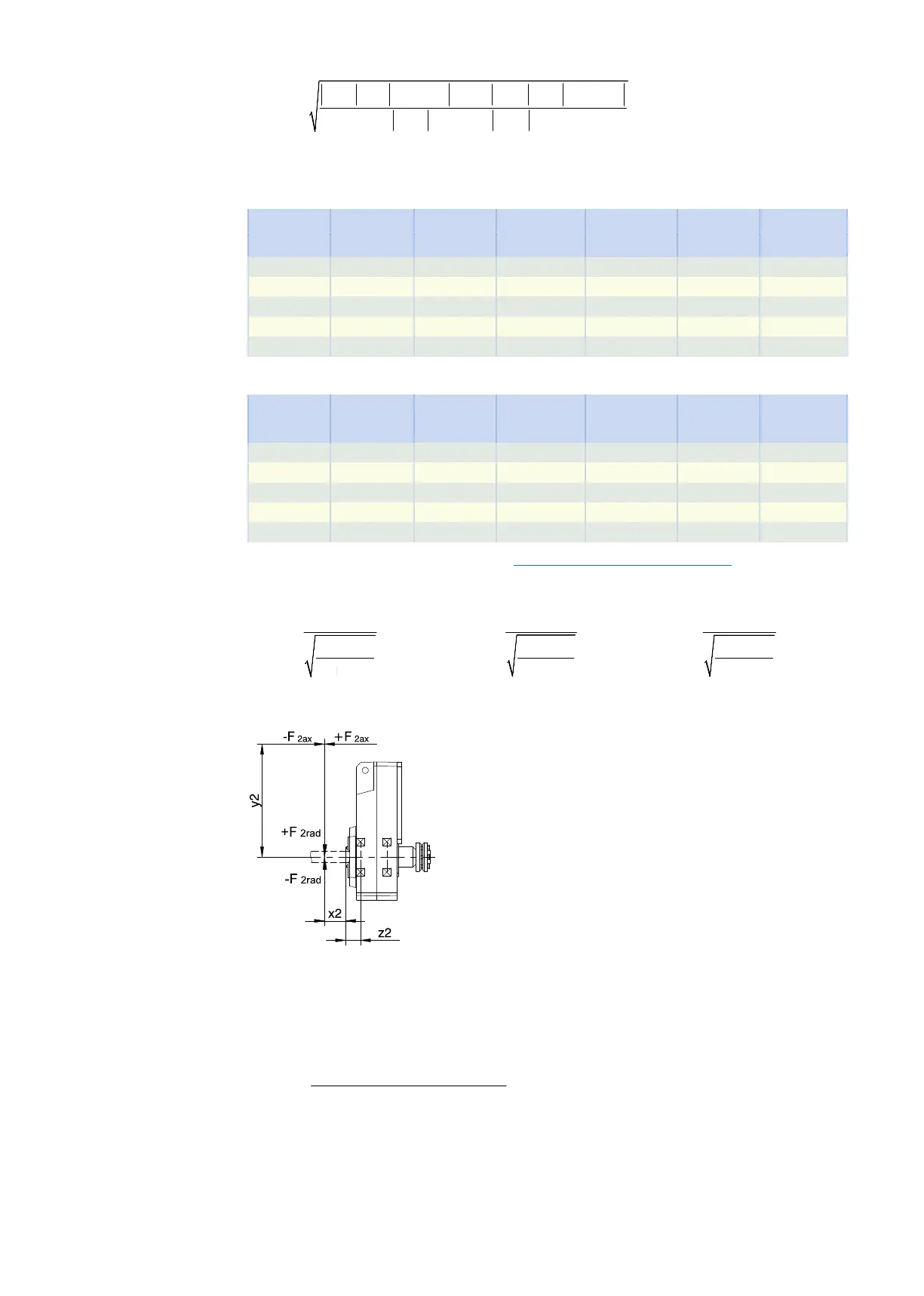
Fig.3: Force application points for hollow shaft
You can determine the permitted radial forces from the permitted tilting torque M
2kN
and M
2k,acc
. The actual
radial forces may not exceed the permitted radial forces. The permitted radial forces pertain to the shaft
end (x2=0).
( )
× × + × +
=
2ax * 2 2rad,acc* 2 2
2k,acc*
2 F y F x z
M
1000
For applications with multiple axial and/or radial forces, you must add the forces as vectors.
In the event of EMERGENCY OFF operation (max. 1000 load changes), you can multiply the permitted forces
and torques for F
2ax20
, F
2rad20
and M
2k20
by a factor of two.
6.6 Project configuration 6 Foffset helical geared motors
182