YASKAWA NX100 Instructions

8.4 ARM Control
8-39
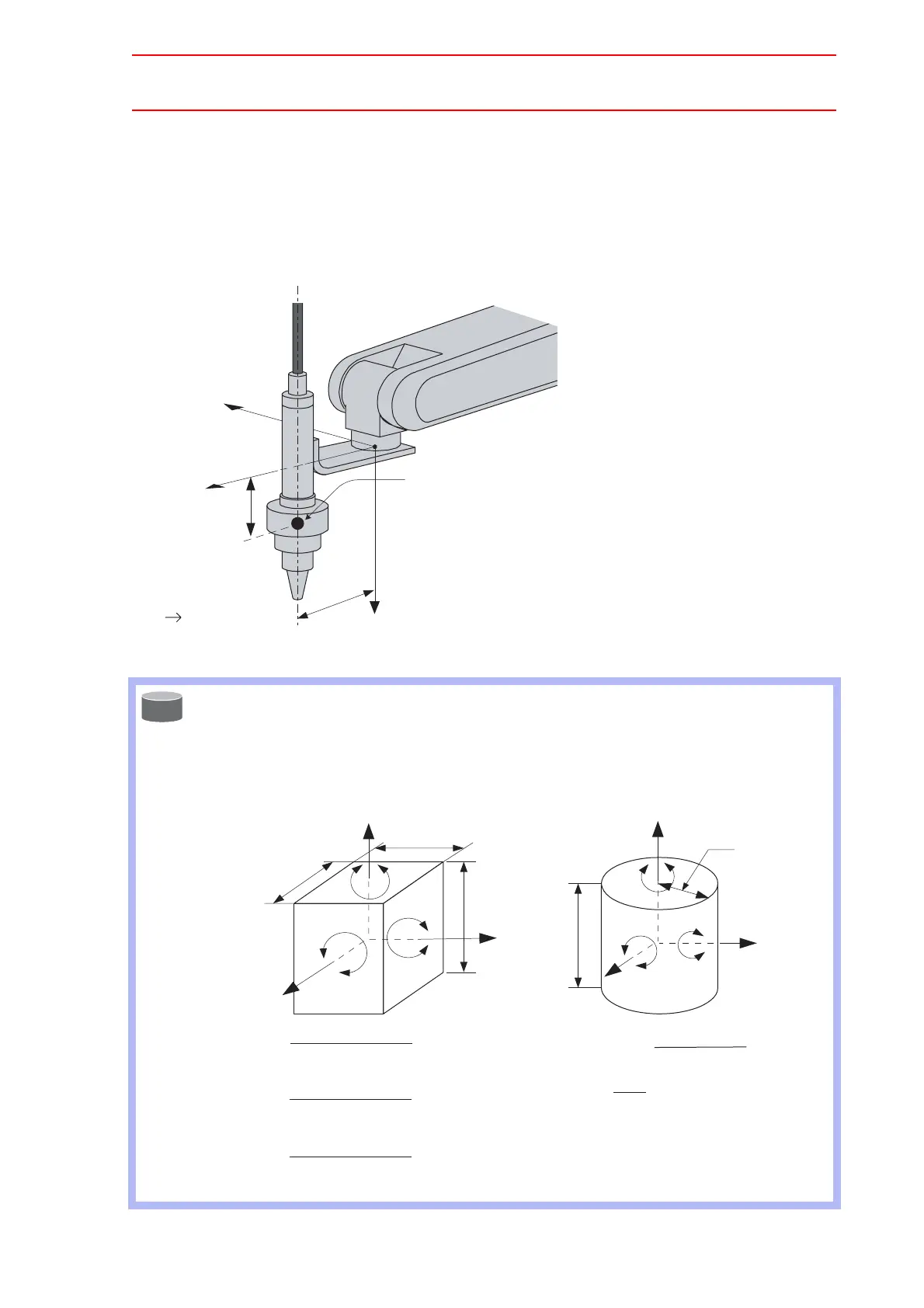
<Example 1>
In the example of sealing gun of the figure below, the center of gravity is set on the flange
coordinates assuming that the center of gravity is positioned slightly inclined to the head from
the center.
There is no need to set the moment of inertia at the center of gravity since the size of the gun
is not too large.
<Setting>
• The own moment of inertia calculation for hexahedron and cylinder
The own moment of inertia
of hexahedron and cylinder can be calculated by the next
expression when the center of gravity is at the center.
Refer to the expression when the calculation of the moment of inertia
at the center of grav-
ity.
Z
F
X
F
Y
F
70
100
Center of Gravity Position
= (100, 0, 70)
Total Weight
Approx. 6.3 [kg]
7.00 [kg]
• W
: 7.000 kg
• Xg
: 100.000 mm
• Yg
: 0.000 mm
• Zg
: 70.000 mm
• Ix
: 0.000 kgm
2
• Iy
: 0.000 kgm
2
• Iz
: 0.000 kgm
2
SUPPLE
-MENT
3 r
2
+ H
2
Ix = Iy = *
W
12
r
2
Iz = * W
2
Ly
2
+ Lz
2
Ix = * W
12
Lx
2
+ Lz
2
Iy = * W
12
Lx
2
+ Ly
2
Iz = * W
12
* Unit of Length : [m]
* Unit of Ix, Iy, Iz : [kg.m
2
]
* Unit of Weight : [kg]
X
Y
Z
Iy
Iz
Ix
Ly
Lx
Weight:W
Lz
H
X
Z
Iz
Ix
r
Weight: W
Iy
Y

YASKAWA NX100 Specifications

General

Manufacturer	YASKAWA
Model	NX100
Operating Temperature	0 to 45°C
Humidity	20 to 80% RH (non-condensing)
Communication Interfaces	Ethernet
Safety Standards	ISO 10218-1
Power Supply	200-230V AC, 50/60Hz
Storage Temperature	60°C