YASKAWA NX100 Instructions

8.4 ARM Control
8-40
<Example 2>
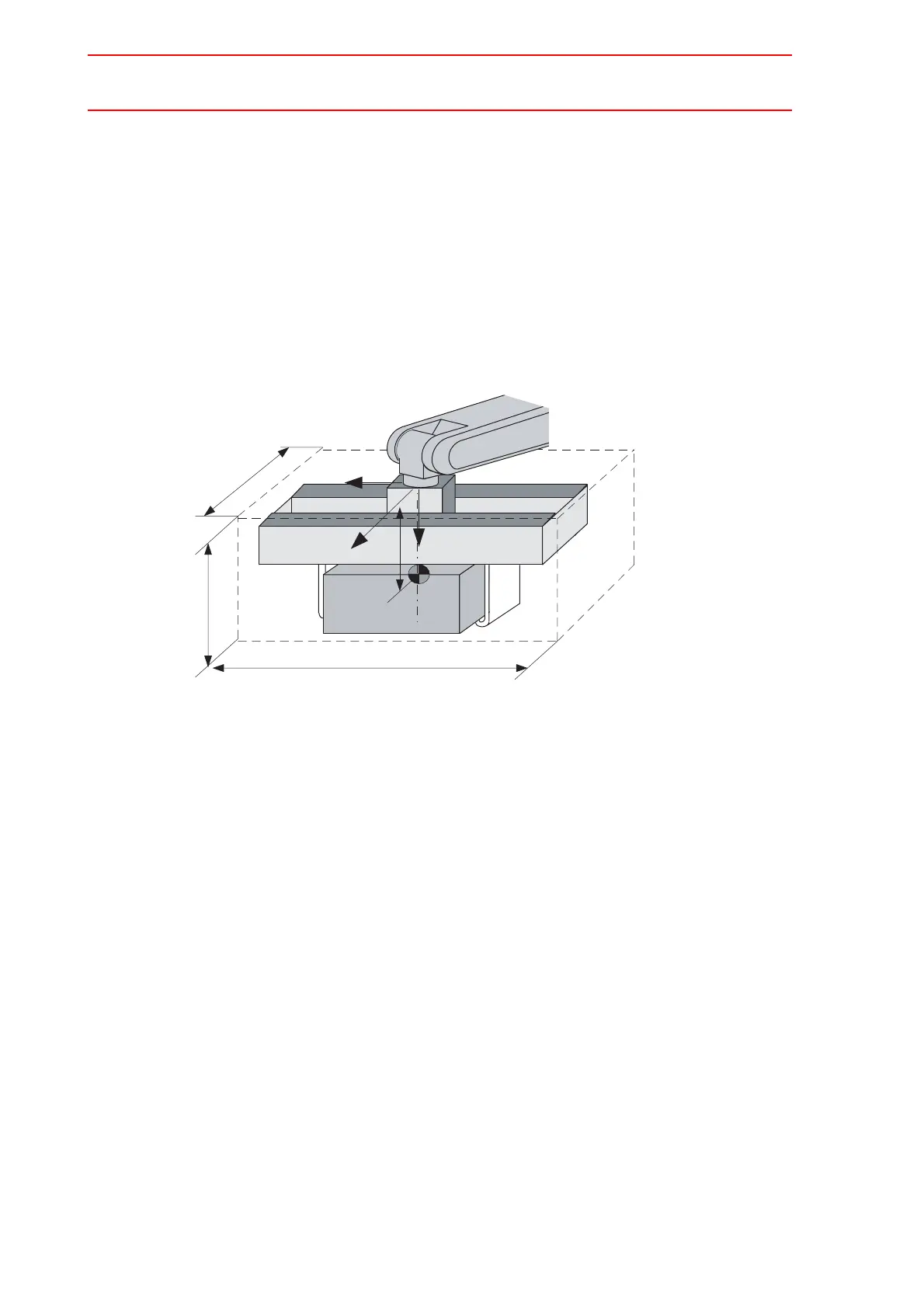
It is necessary to set the moment of inertia at the center of gravity when the entire size of the
tool and workpiece is large compared to the distance from the flange to the center of gravity
position.
Calculate the moment of inertia at the center of gravity roughly from the expression (refer to
the forementioned supplement: "The own moment of inertia calculation for hexahedron and
cylinder"), by approximating the entire tool in the shape of the hexahedron or the cylinder.
If the weight of held workpiece is greatly different in the handling usage etc., it is more effec-
tive to set tool load information on each workpiece and to switch the tool on each step accord-
ing to the held workpiece. Set the tool load information in the state to hold the heaviest
workpiece when using the tools without switching them.
Weight: W = 55 + 40 = 95
= approx. 100[kg]
Center of gravity: Position at flange right under 250mm almost
(Xg, Yg, Zg) = (0,0,250)
Moment of inertia at the center of gravity:
The hexahedron of 0.500 x 0.400 x 1.000[m] which encloses the entire
tool + workpiece is assumed.
By the
expression to calculate the own moment of inertia of hexahedron,
Ix = ( Ly
2
+ Lz
2
/ 12) * W
= ( (0.400
2
+ 1.000
2
) / 12 ) * 100 = 9.667 = approx. 10.000
Iy = ( Lx
2
+ Lz
2
/ 12) * W = ( (0.500
2
+ 0.400
2
) / 12 ) * 100 = 3.417 = approx. 3.500
Iz = ( Lx
2
+ Ly
2
/ 12) * W = ( (0.500
2
+ 1.000
2
) / 12 ) * 100 = 10.417 = approx. 10.500
<Setting>
• W
:
100.000
kg
• Xg
:
0.000
mm
• Yg
:
0.000
mm
• Zg
:
250.000
mm
• Ix
:
10.000
kg.m
2
• Iy
:
3.500
kg.m
2
• Iz
:
10.500
kg.m
2
250
1000
400
500
XF
ZF
YF
Weight of tool:
Approx. 55 kg.
Weight of workpiece:
Approx. 40 kg.

YASKAWA NX100 Specifications

General

Manufacturer	YASKAWA
Model	NX100
Operating Temperature	0 to 45°C
Humidity	20 to 80% RH (non-condensing)
Communication Interfaces	Ethernet
Safety Standards	ISO 10218-1
Power Supply	200-230V AC, 50/60Hz
Storage Temperature	60°C