YOKOGAWA ADMAG TI Series User Manual

<Appendix 5. PID Block>
282
IM 01E21A02-03EN
Index
Parameter
Name
Default
Value
Write
mode
Valid
Range
Description
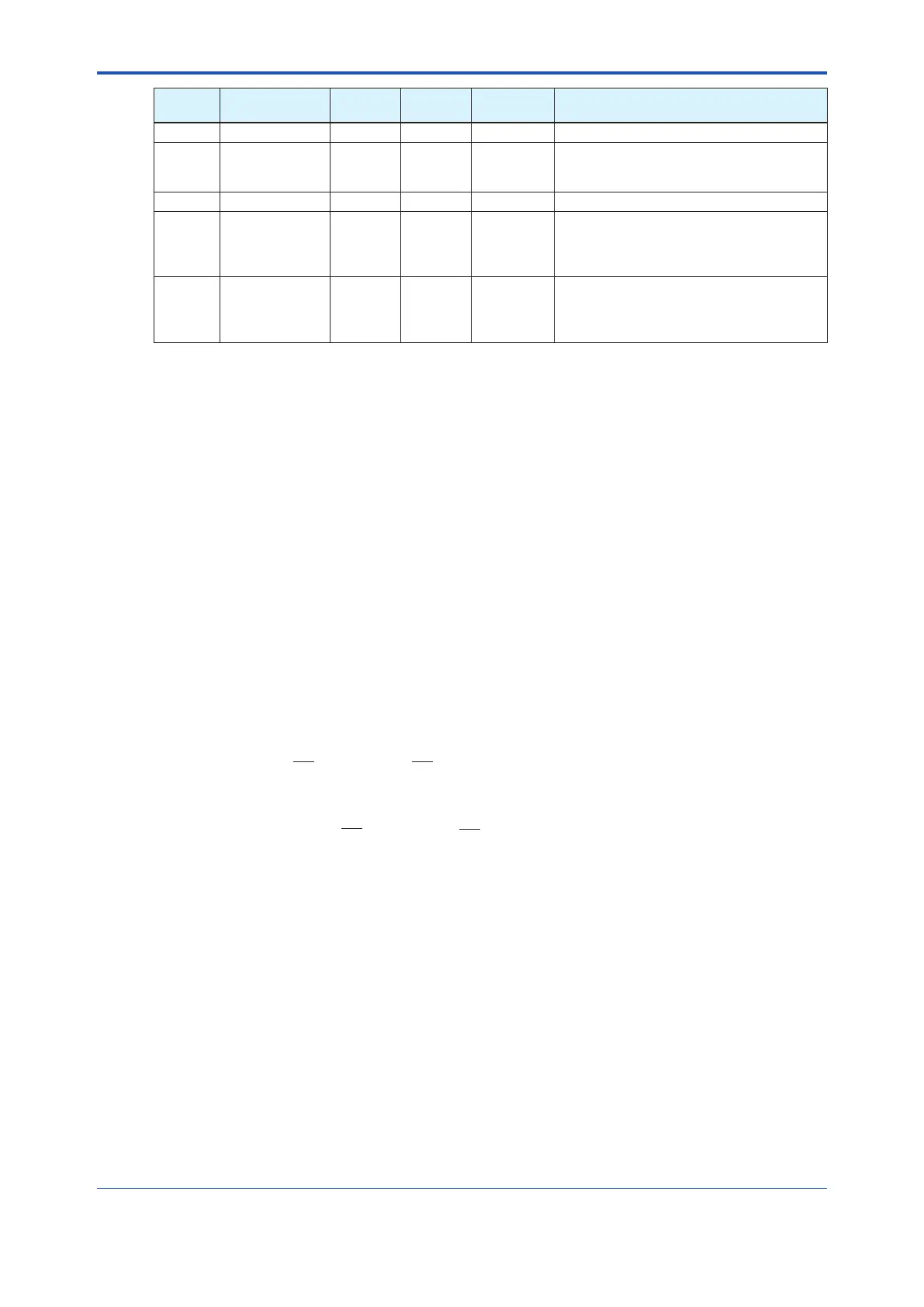
61 HI_ALM --- --- Same as HI_HI_ALM.
62 LO_ALM --- ---
Same as HI_HI_ALM.
Cleared when the PV value increases
aboveLO_LIM+ALM_HYS.
63 LO_LO_ALM --- --- Same as LO_ALM.
64 DV_HI_ALM --- ---
Alarm that is generated when the value of
(PV-SP)hasexceededtheDV_HI_LIM
value. Other features are the same as
HI_HI_ALM.
65 DV_LO_ALM --- ---
Alarm that is generated when the value of
(PV-SP)decreasesbelowtheDV_LO_LIM
value. Other features are the same as
LO_LO_ALM.
A5.4 PID Computation Details
AsthePIDcalculationmethod,theI-PDmethod(PI-Dmethodforsomemodes)isemployed.
A5.4.1 Proportional Derivative Leading Type PID Control
Algorithm (I-PD)
TheproportionalderivativeleadingtypePIDcontrolalgorithm(I-PD)ensurescontrolstability
against sudden changes in the setpoint, such as when the user enters a new setpoint value. At
the same time, the I-PD algorithm ensures excellent controllability by performing proportional,
integral, and derivative control actions in response to changes of characteristics in the controlled
process, changes in load, and occurrences of disturbances. If the mode of the PID block is Auto
and RCas, calculation is done with this I-PD method. When the mode of the block is Cas, the
proportional derivative leading type PID control algorithm is employed in order to obtain better
performance against the changes in the setpoint. The control algorithm is automatically switched
by the block in accordance with the mode.
The basic form of each algorithm is expressed in the equation below.
ΔMVn＝K ΔPVn+ (PVn－SPn)+ Δ(ΔPVn)
ΔT
Ti
Td
ΔT
{ }
比例微分先行形PID（I-PD方式）
微分先行形PID（PI-D方式）
ΔMVn＝K Δ(PVn－SPn)+ (PVn－SPn)+ Δ(ΔPVn)
ΔT
Ti
Td
ΔT
{ }
ΔMVn :changeincontroloutput
ΔPVn :changeinmeasured(controlled)valueΔPVn=PVn-PVn-1
ΔT  :controlperiod(BlockHeader.period_of_execution)
K  :proportionalgain(GAIN)
Ti  :integraltime(RESET)
Td  :derivativetime(RATE)
The subscripts, n and n-1, represent the time of sampling such that PVn and PVn-1 denote the
PV value sampled most recently and the PV value sampled at the preceding control period,
respectively.

YOKOGAWA ADMAG TI Series Specifications

General

Brand	YOKOGAWA
Model	ADMAG TI Series
Category	Measuring Instruments
Language	English