Omron Sysmac NY-series User Manual

4 Exponent Expression
From the previous equation, e-127 = 6. Therefore e = 133.
The number 133 is 10000101 as a binary number
. This expresses the exponent.
5 Mantissa Expression
Numbers following the decimal point in 1.0101
10101 are 010110101.
This number is expressed using 23 bits, but here there are insufficient digits. Therefore zeros
are added. The 23-bit figure becomes f.
Therefore f = 01011010100000000000000.
Therefore, -86.625 is expressed as shown in the following figure.
Man
tissaExponentSign
REAL data (32 bits)
1 10000101
31 30 23 22
01011010100000000000000
0

Valid Ranges
The valid ranges of REAL and LREAL are shown in the following table.
Data type -∞ Negative numbers 0 Positive number +∞
REAL -∞ -3.402823e+38 to -1.175495e-38 0
+1.175495e-38 to +3.402823e
+38
+∞
LREAL -∞
-1.79769313486231e+308 to
-2.22507385850721e-308
0
+2.22507385850721e-308 to
+1.79769313486231e+308
+∞
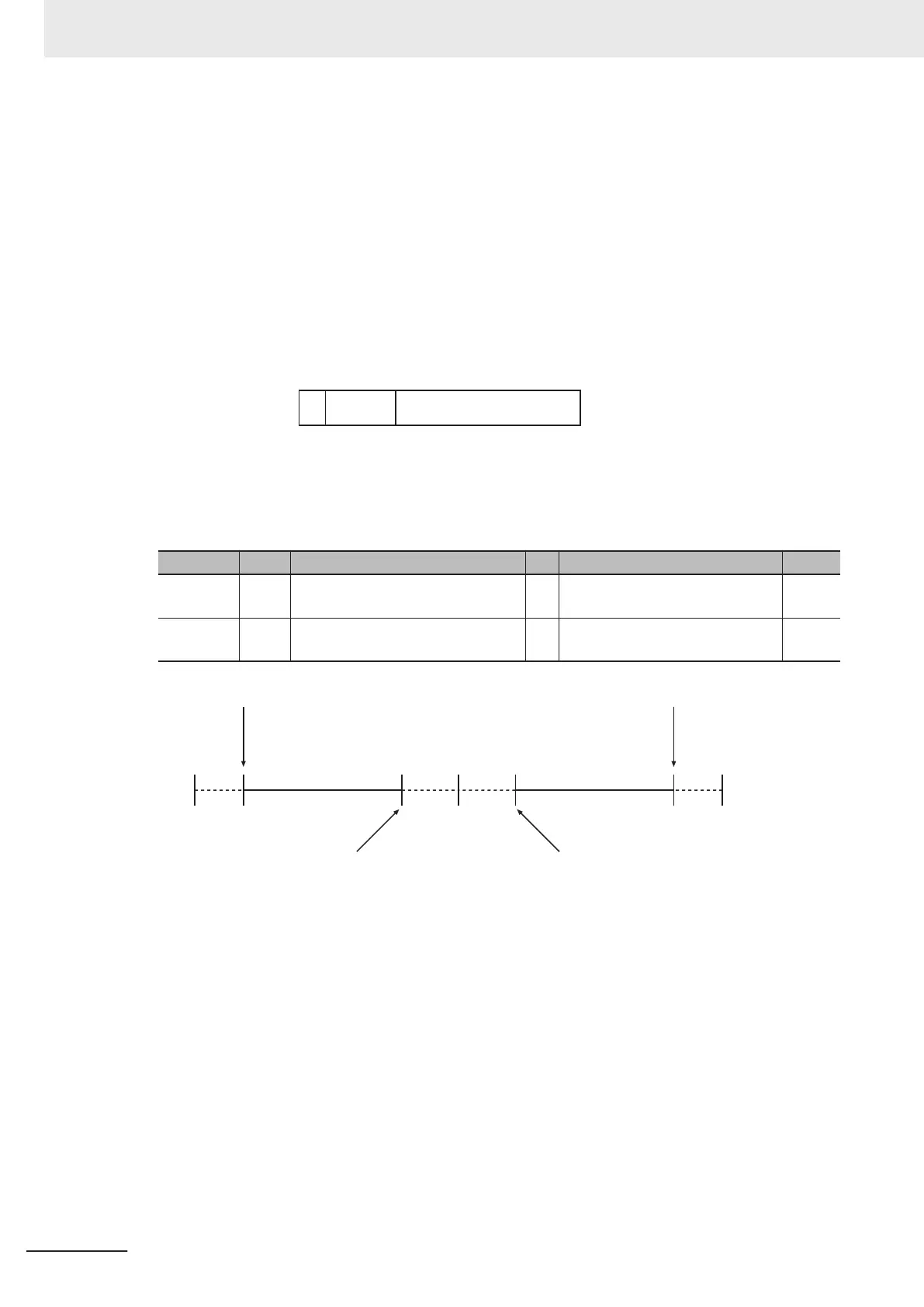
0
−∞
+∞
REAL −3.402823e+38
LREAL −1.79769
313486231e+308
REAL −1.175495e−38
LREAL −2.22507385850721e−308
REAL +1.175495e−38
LREAL +2.22507385850721e−308
REAL +3.402823e+38
LREAL +1.79769313486231e+308

Special Numbers
Positive infinity, negative infinity, +0, -0, and nonnumeric data are called special numbers.
Nonnumeric data is data that cannot be expressed in floating-point decimal format. They are not
treated as numbers.
Mathematically
, +0 and -0 both mean the same as 0, but in data processing it is treated differently.
A detailed explanation is given later.
The sign "s", exponent "e", and mantissa "f" for special numbers take on the following values.
1 Introduction to Motion Control Instructions
1-14
NY-series Motion Control Instructions Reference Manual (W561)

Omron Sysmac NY-series Specifications

General

Brand	Omron
Model	Sysmac NY-series
Category	Control Unit
Language	English