Hioki IM3536 - Page 216

210
Measurement Range and Accuracy
(2) Calculate the basic accuracy for capacitance Cs=160 nF.
(If the measurement conditions are a measurement frequency of 1 kHz and a measurement speed
of SLOW2)
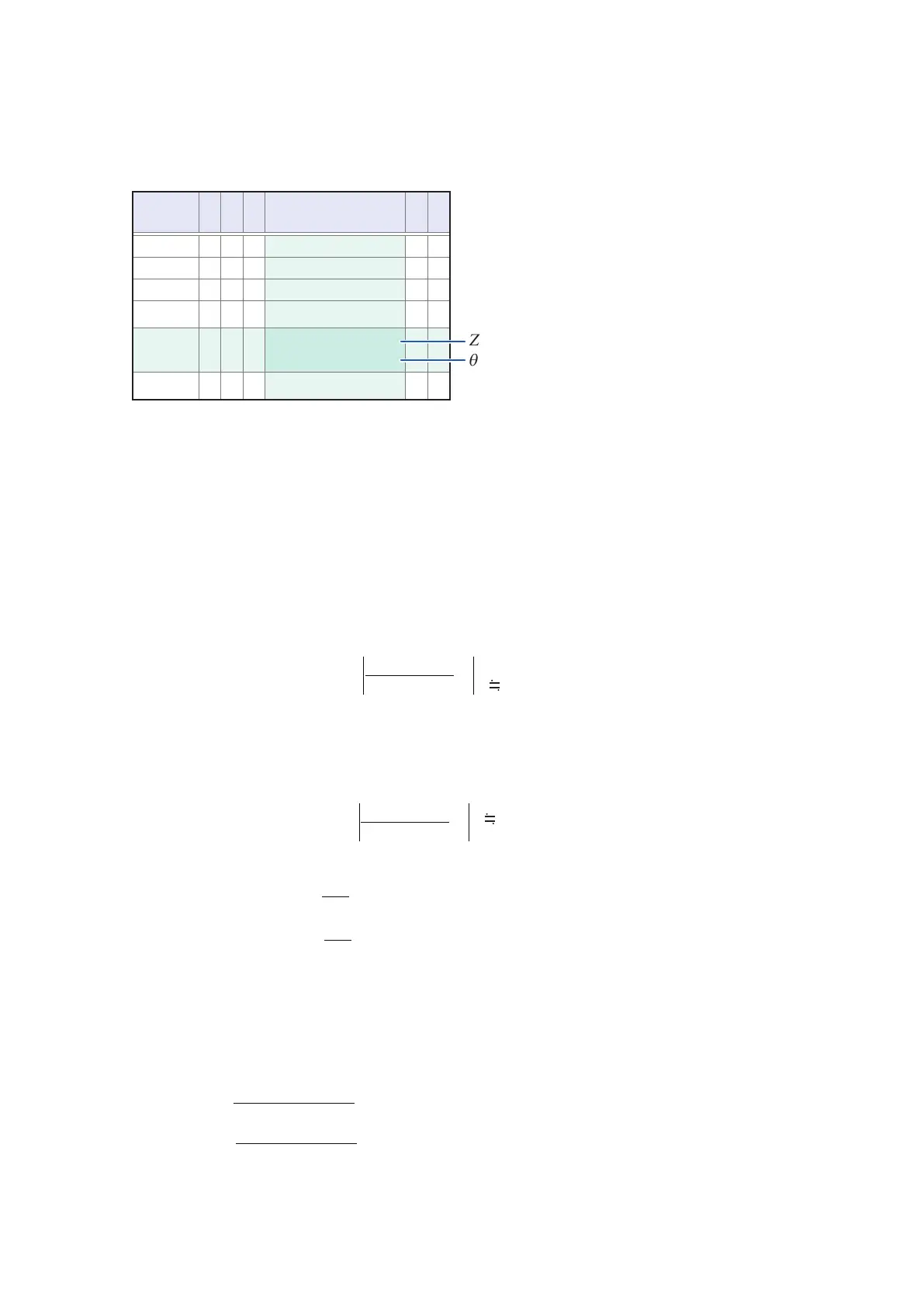
Excerpted from the "Basic accuracy" (p. 207).
Z
θ
Range
1.0000 kHz to
10.000 kHz
100 kΩ
10 kΩ A= 0.05
A= 0.03
B= 0.02
B= 0.02
1 kΩ
1
Measure the sample’s Z and θ values using auto-ranging.
Assume that the measured Z and
θ values are as follows:
Z =1.0144 k
Ω
, θ =-78.69°
Because
Z is 1.0144 kΩ, 10 kΩ measurement range will be used.
2
Find the cell at the intersection of the row for the 10 kΩ range and the 1.0000 kHz to
10.000 kHz column (since the measurement frequency is 1 kHz) in the "Basic accuracy"
(p. 207).
3
Calculate the basic accuracy for Z using the Z coefcients A and B.
Based on the accuracy table, coefcient A = 0.05 and coefcient B = 0.02
Plug in the values for the 1 k
Ω
range in the "Basic accuracy" (p. 207) into the follow-
ing equation:
Z accuracy =
10 10.144
0.05 0.02 1
10
k
k
 × Ω 
± + × −
 
Ω
 
0.05% rdg.
4
Similarly, calculate the basic accuracy of θ .
The accuracy table yields the values A=0.03 and B=0.02
Using the basic accuracy formula of "Basic accuracy" (p. 207) for "1 k± or more".
θ accuracy =
10 10.144
0.03 0.02 1
10
k
k
 × Ω 
± + × −
 
Ω
 
±0.03°
5
Calculate the range within which Z and θ values can be acquired from the basic accuracy.
0.05
min 1.0144 1 1.0139
100
0.05
max 1.0144 1 1.0149
100
min 78.69 0.03 78.72
max 78.69 0.03 78.66
Z k k
Z k k
θ
θ
 
= Ω× − Ω
 
 
 
= Ω× + Ω
 
 
= − − = − °
= − + = − °
≒
≒
6
Calculate the range within which Cs values can be acquired based on the Z and θ ranges.
(For more information about the Cs calculation formula, see "Appx. 1 Measurement Param-
eters and Calculation Formula" (p. Appx.1).)
3
3
3
3
10×1.0144×10
Z = 0.05+0.02× -1 0.05%
10×10
10×1.0144×10
= 0.03+0.02× -1 0.03
10×10
0.05
min 1.0144 × 1- 1.0139
100
0.05
max 1.0144 × 1- 1.0149
100
min 78.69 0.
Z k k
Z k k
θ
θ
 
± ±
 
 
 
 
± ± °
 
 
 
 
= Ω Ω
 
 
 
= Ω Ω
 
 
= − −
基本確度 ≒
基本確度 ≒
≒
≒
03 78.72
max 78.69 0.03 78.66
1
min 159.90nF ... 0.0625% rdg.
×Zmax×sin min
1
max 160.10nF ... 0.0625% rdg.
×Zmin×sin max
2
Cs
Cs
f
θ
ϖ θ
ϖ θ
ϖ π
= − °
= − + = − °
= −
=
= × ×
≒
≒
f
is frequency [Hz].
Consequently, the Cs basic accuracy is ± 0.0625% rdg.