ST STM32G474 User Manual

CORDIC co-processor (CORDIC) RM0440
478/2126 RM0440 Rev 4
17.3.6 Zero-overhead mode
The fastest way to use the co-processor is to pre-program the CORDIC_CSR register with
the function to be performed (FUNC), the desired number of clock cycles (PRECISION), the
size of the input and output values (ARGSIZE, RESSIZE), the number of input arguments
(NARGS) and/or results (NRES), and the scaling factor (SCALE), if applicable.
Subsequently, a calculation is triggered by writing the input arguments to the
CORDIC_WDATA register. As soon as the correct number of input arguments has been
written (and any ongoing calculation has finished) a new calculation is launched using these
input arguments and the current CORDIC_CSR settings. There is no need to re-program
the CORDIC_CSR register if there is no change.
If a dual 32-bit input argument is needed (ARGSIZE = 0, NARGS = 1), the primary input
argument, ARG1, must be written first, followed by the secondary argument, ARG2. If the
secondary argument remains unchanged for a series of calculations, the second write can
be avoided, by reprogramming the number of arguments to one (NARGS = 0), once the first
calculation has started. The secondary argument retains its programmed value as long as
the function is not changed.
Note: ARG2 is set to +1 (0x7FFFFFFF) after a reset.
If two 16-bit arguments are used (ARGSIZE = 1) they must be packed into a 32-bit word,
with ARG1 in the least significant half-word and ARG2 in the most significant half-word. The
packed 32-bit word is then written to the CORDIC_WDATA register. Only one write is
needed in this case (NARGS = 0).
For functions which take only one input argument, ARG1, it is recommended to set
NARGS = 0. If NARGS = 1, a second write to CORDIC_WDATA must be performed to
trigger the calculation. The ARG2 data in this case is not used.
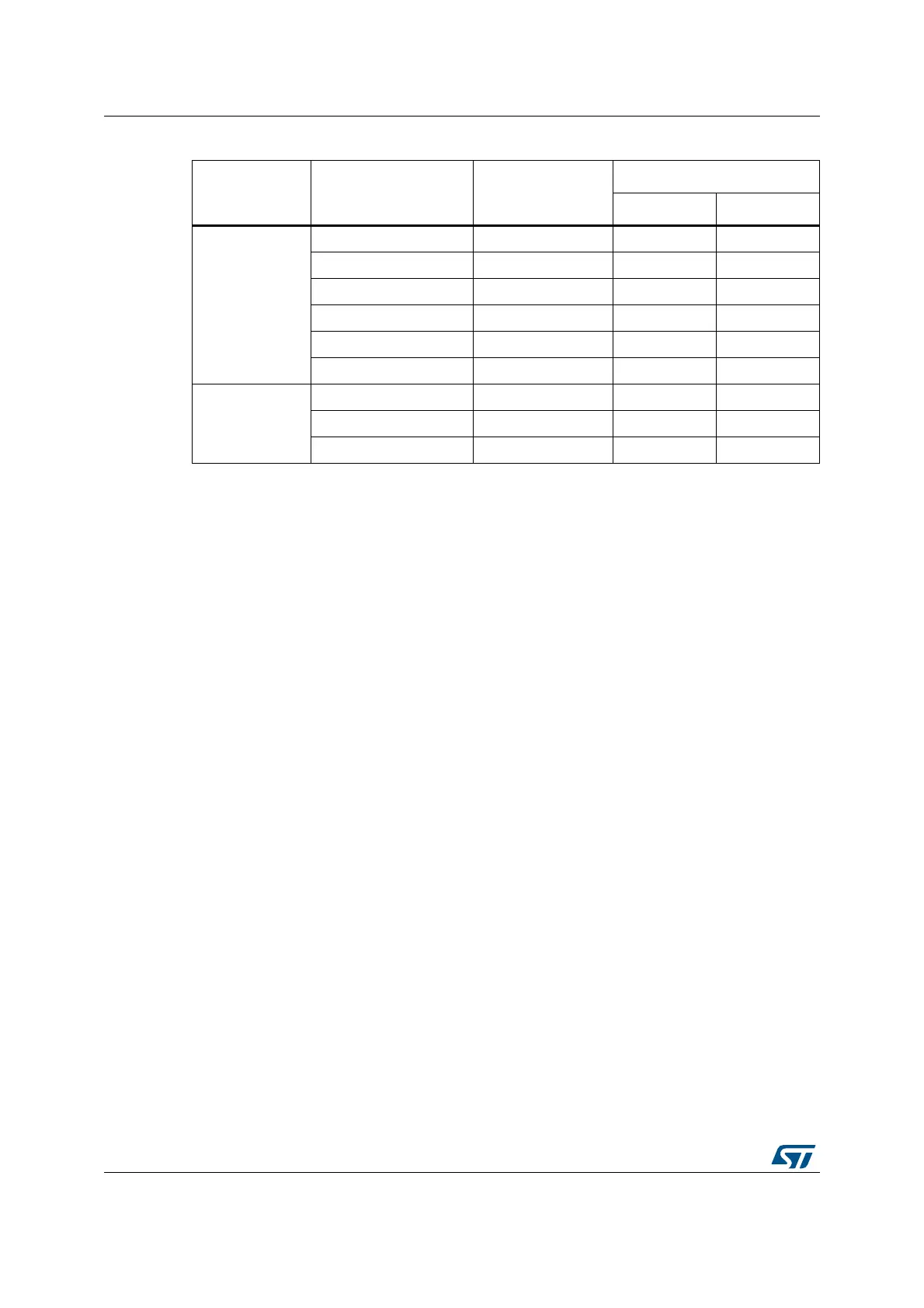
Sinh, Cosh,
Atanh, Ln
(3)
412
-2
2
-2
822
-6
2
-6
12 3 2
-10
2
-10
16 4 2
-13
2
-13
20 5 2
-17
2
-15
24 6 2
-18
2
-15
Sqrt
(4)
412
-7
2
-7
822
-14
2
-14
12 3 2
-19
2
-15
1. Max residual error is the maximum error remaining after the given number of iterations, compared to the
identical calculation performed in double precision floating point. An additional rounding error may be
incurred, of up to 2
-16
for q15 format or 2
-20
for q31 format.
2. For modulus > 0.5. The achievable precision reduces proportionally to the magnitude of the modulus, as
quantization error becomes significant.
3. SCALE = 1. If a higher scaling factor is used, the achievable precision is reduced proportionally.
4. SCALE = 0. If a higher scaling factor is used, the achievable precision is reduced proportionally.
Table 115. Precision vs. number of iterations (continued)
Function
Number of
iterations
Number of
cycles
Max residual error
(1)
q1.31 format q1.15 format

ST STM32G474 Specifications

General

Brand	ST
Model	STM32G474
Category	Microcontrollers
Language	English