App-19
IM 701450-01E
App
Appendix
Hilbert Function (HLBT)
Normally, when we analyze a real time signal, it is convenient to think of this signal as
the real part of a complex function and do the actual analysis using the complex function.
If the real time signal is considered to be the real part of the function, the imaginary part
can be determined with the Hilbert transform of the real part. The Hilbert transform does
not change the order of the individual variables. Hilbert transform of a time signal results
in another time signal. The Hilbert transform is described below. When transforming a
signal in the time domain, the signal is transformed into the frequency domain, first,
using the Fourier transform. Next, the phase of each frequency component is shifted by
–90 deg if the frequency is positive and +90 deg if negative. Lastly, taking the inverse
Fourier transform completes the Hilbert transform.
Example
• Hilbert transform can be used to analyze an envelope waveform.
AM (amplitude modulation): SQRT(C1×C1+HLBT(C1)×HLBT(C1))
Demodulation of a FM signal: DIF(PH(C1,HLBT(C1)))
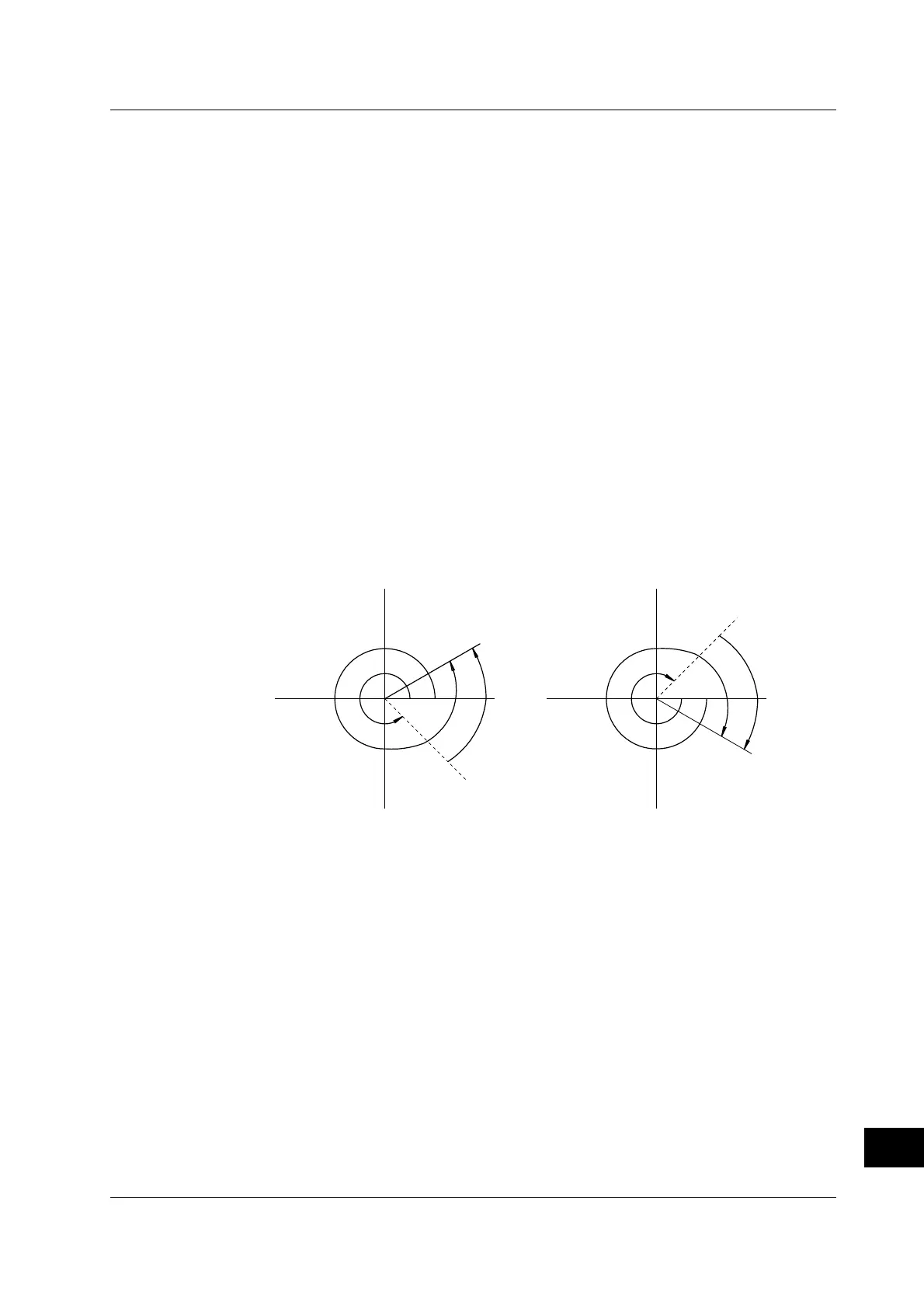
Phase Function (PH)
Phase function PH(X1,Y1) computes tan
–1
(X1/Y1). However, the phase function takes
the phase of the previous point into consideration and continues to sum even when the
value exceeds ±π (ATAN function reflects at ±π).
The unit is radians.
Preceding Point
Preceding Point
θ2
θ2
θ2=θ1+∆θ2 θ2=θ1-∆θ2
∆θ2
∆θ2
θ1
θ1
Appendix 4 User-Defined Computation
To Next Page
Loading...
Need help?
General
