Agilent Technologies 35670A User Manual

To calculate the envelope of a function
1 Press [
Analys
][
DEFINE FUNCTION
].
Define the Hilbert transform in [
FUNCTION F1
].
2 Press [
DEFINE F2
].
Press [
MEAS DATA
][
TIME CHANNEL 1
][
*
].
Press [
CONSTANT (K1-K5)
][
CONSTANT K1
][
+
].
3 Press [
(
][
FUNCTION (F1-F5)
][
FUNCTION F1
][
*
][
CONSTANT (K1-K5)
][
CONSTANT K4
].
Press [
ENTER
].
4 Press [
Meas Data
][
MORE CHOICES
][
MATH FUNCTION
][
F2
].
5 Press [
Trace Coord
][
LINEAR MAGNITUDE
].
The Hilbert transform is called a poor man’s demodulation because you can use it to
study the envelope of a modulating signal. In addition, you can determine system
delays by identifying peak positions of the magnitude.
The envelope function is the linear magnitude of the analytic signal. The linear
magnitude trace coordinate is the square root of the sum of the squares of the real and
imaginary components. The analytic signal is the sum of f(t)+jf
~
(t),where jf
~
(t) is
the Hilbert transform.
This task calculates the envelope function by using the Hilbert transform. The
procedure utilizes the predefined constant registers:
0s 7.8049ms
A: CH1Time
25
mV
-25
mV
Real
5
mV
/div
B: F2 TIME1*K1+(
20
mV
0
V
LinMag
2
mV
/div
0s 7.8049ms
F1 = IFFT (K5*FFT (TIME1)
F2=TIME1*K1+(F1*K4)
F3 =
F4 =
F5 =
K1 = 1.000000 + j 0.000000
K2=
K3=
K4 = 0.000000 + j 1.000000
K5 = 0.000000 - j 1.000000
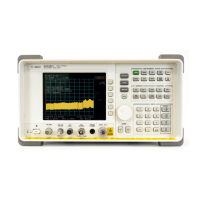
Trace A shows the modulating signal.
Trace B shows the envelope of the
signal in Trace A.
Agilent 35670A
Operator's Guide Math Operations and Data Editing
18-11

Agilent Technologies 35670A Specifications

General

Brand	Agilent Technologies
Model	35670A
Category	Measuring Instruments
Language	English