Agilent Technologies 35670A

Cycle power. Set up the analyzer and the device-under-test for a frequency response
measurement with RMS averaging.
Press [
Analys
][
DEFINE FUNCTION (F1-F5)
][
DEFINE F1
].
Press [
MEAS DATA
][
COHERENCE 2/1
].
Press [
/
][
(
].
Press [
CONSTANT (K1-K5)
][
CONSTANT K1
].
Press [
+
][
(
].
Press [
CONSTANT (K1-K5)
][
CONSTANT K3
]
Press [
*
].
Press [
MEAS DATA
][
COHERENCE 2/1
].
Press [
ENTER
].
Press [
Meas Data
][
MORE CHOICES
][
MATH FUNCTION
][
F1
].
Press [
Trace Coord
][
MORE CHOICES
][
REAL PART
].
Press [
Scale
][
AUTOSCALE ON OFF
] to highlight ON.
The signal-to-noise (S/N) ratio versus frequency is calculated from the coherence
function. The signal power spectrum is G
yy
and true noise is G
nn
.
The coherence value γ
2
(f) has a range of 0.0 to +1.0 which corresponds to a
signal-to-noise range of 0 to infinity.
The S/N ratio is computed by dividing the coherence data by the product of
multiplying the coherence, a real number, by minus one and then adding one.
This task utilizes the predefined constant registers. [
CONSTANT K1
] contains a positive
one (+1); [
CONSTANT K3
] contains a negative one (-1).
Sf
Nf
Gyy f
Gnn f
yf
yf
()
()
()
()
()
()
==
−
2
1
2
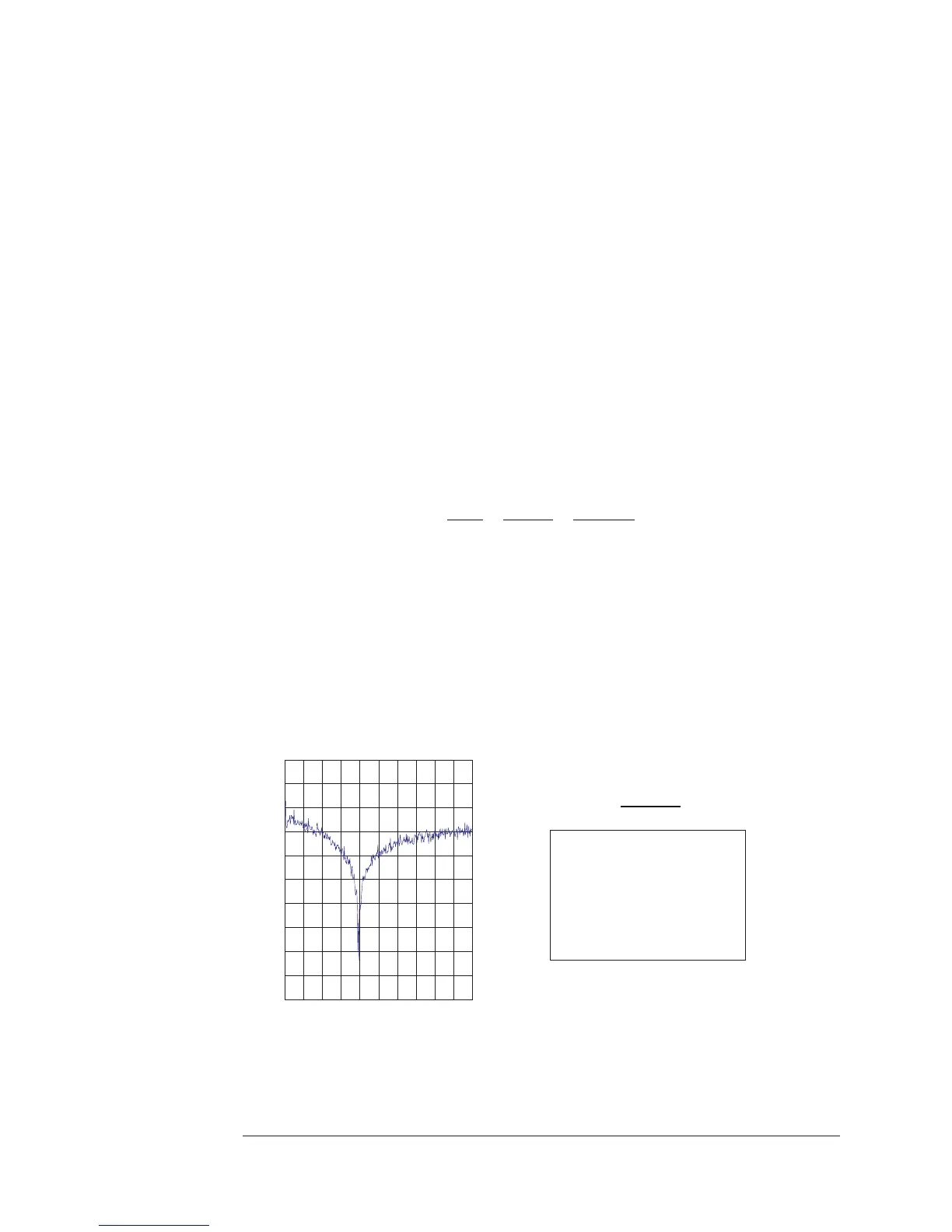
A: F1 COH21/(K1+ X:1.344 kHz Y:32.1018dB
0Hz 12 8kHzAVG: 10
60
dB
-40
dB
dBMag
10
dB
/div
MeasData
[FFT]
A: F1 B: FreqResponse
C: Coherence D: F3
F1=COH21/(K1+(K3*COH21))
F2 =
F3 =
F4 =
F5 =
K1 = 1.000000 + j 0.000000
K2 = 2.000000 + j 0.000000
K3 = -1.000000 + j 0.000000
K4 = 0.000000 + j 1.000000
K5 = 0.000000 - j 1.000000
F1 reads as
COH21
(1−COH21)
Agilent 35670A
Math Operations and Data Editing Operator's Guide
18-12