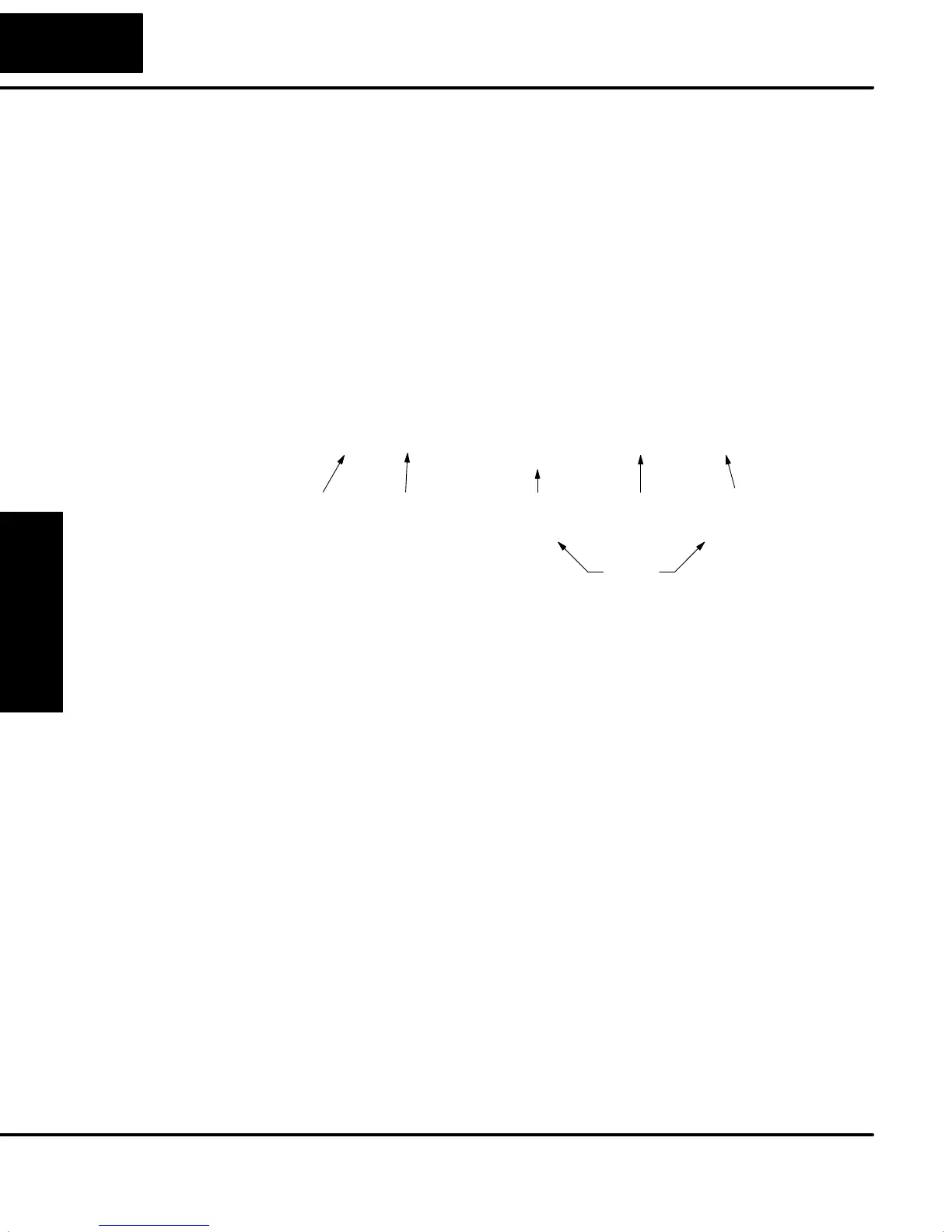PID Loop Operation
Maintenance
and Troubleshooting
8–32
PID Loop Operation
The position algorithm variables and related variables are:
T
s = Sample rate
K
c = Proportional gain
K
i = Kc * (Ts/Ti) coefficient of integral term
K
r = Kc * (Td/Ts) coefficient of derivative term
T
i = Reset time (integral time)
T
d = Rate time (derivative time)
SP
n = Set Point for sampling time “n” (SP value)
PV
n = Process variable for sampling time “n” (PV)
e
n = SPn – PVn = Error term for sampling time “n”
M
0 = Control Output for sampling time “0”
M
n = Control Output for sampling time “n”
Analysis of these equations will be found in most good text books on process control.
At a glance, we can isolate the parts of the PID Position Algorithm which correspond
to the P, I, and D terms, and the Bias as shown below.
S
Mn = Kc * en + Ki * ei + Kr * (en – en–1) + Mo
i=1
n
Control
Output
Proportional
Term
Initial
Output
Integral
Term
Derivative
Term
Bias
Term
The initial output is the output value assumed from Manual mode control when the
loop transitioned to Auto Mode. The sum of the initial output and the integral term is
the bias term, which holds the “position” of the output. Accordingly, the Velocity
Algorithm discussed next does not have a bias component.
The Velocity Algorithm form of the PID equation can be obtained by transforming
Position Algorithm formula with subtraction of the equation of (n–1)th degree from
the equation of nth degree.
The velocity algorithm variables and related variables are:
T
s = Sample rate
K
c = Proportional gain
K
i = Kc * (Ts/Ti) = coefficient of integral term
K
r = Kc * (Td/Ts) = coefficient of derivative term
T
i = Reset time (integral time)
T
d = Rate time (derivative time)
SP
n = Set Point for sampling time “n” (SP value)
PV
n = Process variable for sampling time “n” (PV)
e
n = SPn – PVn = Error term for sampling time “n”
M
n = Control Output for sampling time “n”
The resulting equations for the Velocity Algorithm form of the PID equation are:
DMn = Kc * (en – en–1) + Ki * en + Kr * (en – 2*en–1 +en–2)
DMn =Mn – Mn–1
Velocity Algorithm
To Next Page
Loading...
Need help?
General
