Schweitzer Engineering Laboratories SEL-421-4 - Figure 5.69 Tilt in Apparent Fault Impedance Resulting from Nonhomogeneity

5.88
SEL-421 Relay Instruction Manual Date Code 20171021
Protection Functions
Quadrilateral Phase-Distance Elements
A network is homogeneous with respect to the particular fault location if
Equation 5.29 is satisfied:
Equation 5.29
If Equation 5.29 is not satisfied, use Equation 5.30 to determine the negative-
sequence nonhomogeneity:
Equation 5.30
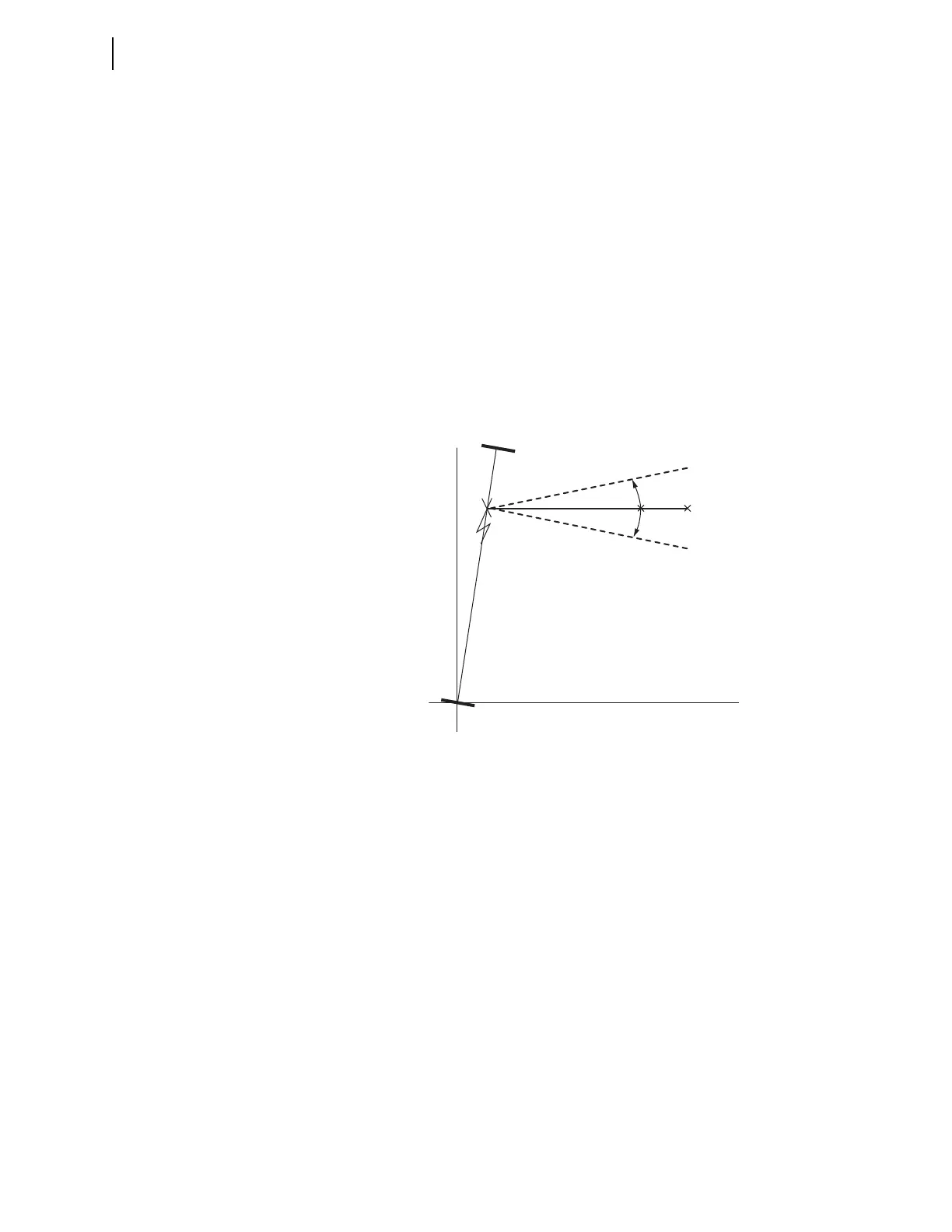
The value of T represents how much the apparent fault impedance (ZF) measured
by the relay tilts up or down (electrical degrees) because of the nonhomogeneity
of the corresponding network for a fault at location m (see Figure 5.69).
Calculate T for a phase-to-phase fault at the remote bus (i.e., m equals one per
unit). The remote bus is selected for the fault location to prevent Zone 1 phase-
distance element overreach.
Each quadrilateral phase-distance element is supervised by the corresponding
Relay Word bit ENX2AB, ENX2BC, or ENX2CA during unbalanced fault con-
ditions (32QE = 1). This supervisory condition secures the reactance element in
the quadrilateral phase-distance element against unusual unbalanced load condi-
tions where currents (but not voltages) are unbalanced.
A supervisory condition is applied to force the right-resistive blinders to be self-
polarized under the previous unusual unbalanced loads. The adaptability of the
positive-sequence polarized resistive blinder is enabled during balanced operat-
ing conditions (32QE = 0). This adaptability is also enabled during unbalanced
fault conditions (32QE = 1) when the corresponding Relay Word bit CNR1AB,
CNR1BC, or CNR1CA is asserted. The adaptability of the negative-sequence
polarized resistive blinder is enabled during unbalanced fault conditions
(32QE = 1) when the corresponding Relay Word bit CNR2AB, CNR2BC, or
CNR2CA is asserted. When the adaptability of any of the right resistive blinders
is disabled, the corresponding blinder uses self polarization.
Figure 5.69 Tilt in Apparent Fault Impedance Resulting From Nonhomogeneity
X
LEFT
R
LEFT
--------------
X
RIGHT
R
RIGHT
----------------=
T
Z1S Z1L Z1R++
1m–Z1L Z1R+•
-----------------------------------------------------


arg=
XR
R
S
F
+T
—T
Z
F