7.3.4. Slip compensation
In case of a load, the speed of an asynchronous motor decreases. This load-dependent
speed drop is called slip. The slip compensation serves to counteract the load-dependent
speed loss.
Preconditions
The function is only effective in the motor control type "V/f characteristic control (VFC
open loop)".
In order that the function can determine the rated slip correctly, the following parameters
must be set correctly:
• Rated speed
• Rated frequency
• Number of pole pairs (automatically calculated from Rated speed and Rated
frequency)
Details
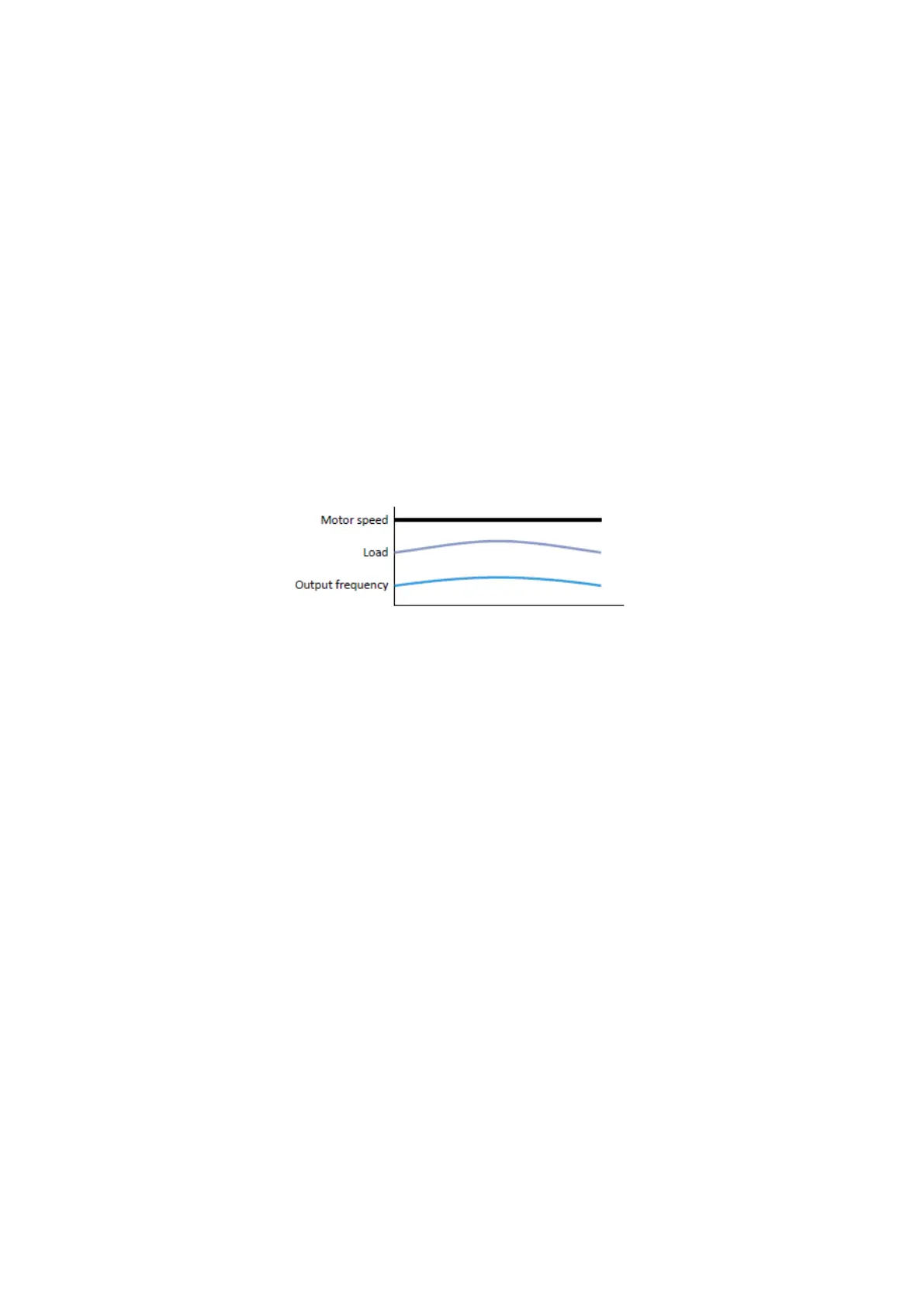
The slip compensation increases or decreases the output frequency as a response to a
load change. Thus, the slip is counteracted and the speed is kept precisely.
The rated slip required for the slip compensation is calculated by the inverter according to
the following formula:
Rated slip [%] = (1 (rated motor speed [rpm] / (120 * rated motor frequency [Hz] / number
of poles))) * 100
Calculation example:
• Rated motor speed = 1750 rpm
• Rated motor frequency = 60 Hz
• Number of poles = 2 * Number of pole pairs = 2 * 2 = 4
• Rated slip = (1 (1750 / (120 * 60 / 4))) * 100 = 2.77 %
The rated slip represents the reduction of the motor speed due to the motor load. At full
speed and full load, the motor given in the example would rotate with 1750 rpm, which
means 2.77 % below its synchronous speed of 1800 rpm. In order to compensate this
speed loss, the inverter increases the output frequency by the rated slip multiplied by the
rated motor frequency. In the example 2.77 % * 60 Hz = 1.66 Hz increase at full load.
In order to consider load changes, the influence of the rated slip on output frequency can
be adapted in 0x2B09:001 (P315.01). A setting of 100 % corresponds to the rated slip of
the machine in the nominal operating point.
With reference to the example above and a setpoint frequency of 60 Hz:
• If 0x2B09:001 (P315.01) = 100 %, the output frequency is = 61.66 Hz (60 Hz + 100 % *
1.66 Hz).
• If 0x2B09:001 (P315.01) = 50 %, the output frequency is = 60.83 Hz (60 Hz + 50 % *
1.66 Hz).
 Loading...
Loading...