Infineon TriCore TC1.6P User Manual

TriCore
®
TC1.6P & TC1.6E
32-bit Unified Processor Core
Instruction Set
V1.0 2013-07
User Manual (Volume 2) 3-285
MULR.H
Packed Multiply Q Format with Rounding
Description
Multiply two signed 16-bit (half-word) values. Add the product (left justified if n == 1) to a signed 16-bit value and
put the rounded result into half of a 32-bit register. Note that since there are two results the two register halves are
used). There are four cases of half-word multiplication:
• 16U * 16U, 16L * 16L
• 16U * 16L, 16L * 16U
• 16U * 16L, 16L * 16L
• 16L * 16U, 16U * 16U
Note that n should only take the values 0 or 1, any other value returns an undefined result. If (n == 1) then 8000
H
* 8000
H
= 7FFFFFFF
H
(for signed 16-bit * 16-bit multiplications only).
MULR.HD[c], D[a], D[b] LL, n (RR1)
(16U * 16L || 16L * 16L) rounded --> 16||16
sc1 = (D[a][31:16] == 8000
H
) AND (D[b][15:0] == 8000
H
) AND (n == 1);
sc0 = (D[a][15:0] == 8000
H
) AND (D[b][15:0] == 8000
H
) AND (n == 1);
result_halfword1 = sc1 ? 7FFFFFFF
H
: (((D[a][31:16] * D[b][15:0]) << n) + 8000
H
);
result_halfword0 = sc0 ? 7FFFFFFF
H
: (((D[a][15:0] * D[b][15:0]) << n) + 8000
H
);
D[c] = {result_halfword1[31:16], result_halfword0[31:16]}; // Packed short fraction
MULR.HD[c], D[a], D[b] LU, n (RR1)
(16U * 16L || 16L * 16U) rounded --> 16||16
sc1 = (D[a][31:16] == 8000
H
) AND (D[b][15:0] == 8000
H
) AND (n == 1);
sc0 = (D[a][15:0] == 8000
H
) AND (D[b][31:16] == 8000
H
) AND (n == 1);
result_halfword1 = sc1 ? 7FFFFFFF
H
: (((D[a][31:16] * D[b][15:0]) << n) + 8000
H
);
result_halfword0 = sc0 ? 7FFFFFFF
H
: (((D[a][15:0] * D[b][31:16]) << n) + 8000
H
);
D[c] = {result_halfword1[31:16], result_halfword0[31:16]}; // Packed short fraction
MULR.HD[c], D[a], D[b] UL, n (RR1)
(16U * 16U || 16L * 16L) rounded --> 16||16
sc1 = (D[a][31:16] == 8000
H
) AND (D[b][31:16] == 8000
H
) AND (n == 1);
sc0 = (D[a][15:0] == 8000
H
) AND (D[b][15:0] == 8000
H
) AND (n == 1);
result_halfword1 = sc1 ? 7FFFFFFF
H
: (((D[a][31:16] * D[b][31:16]) << n) + 8000
H
);
result_halfword0 = sc0 ? 7FFFFFFF
H
: (((D[a][15:0] * D[b][15:0]) << n) + 8000
H
);
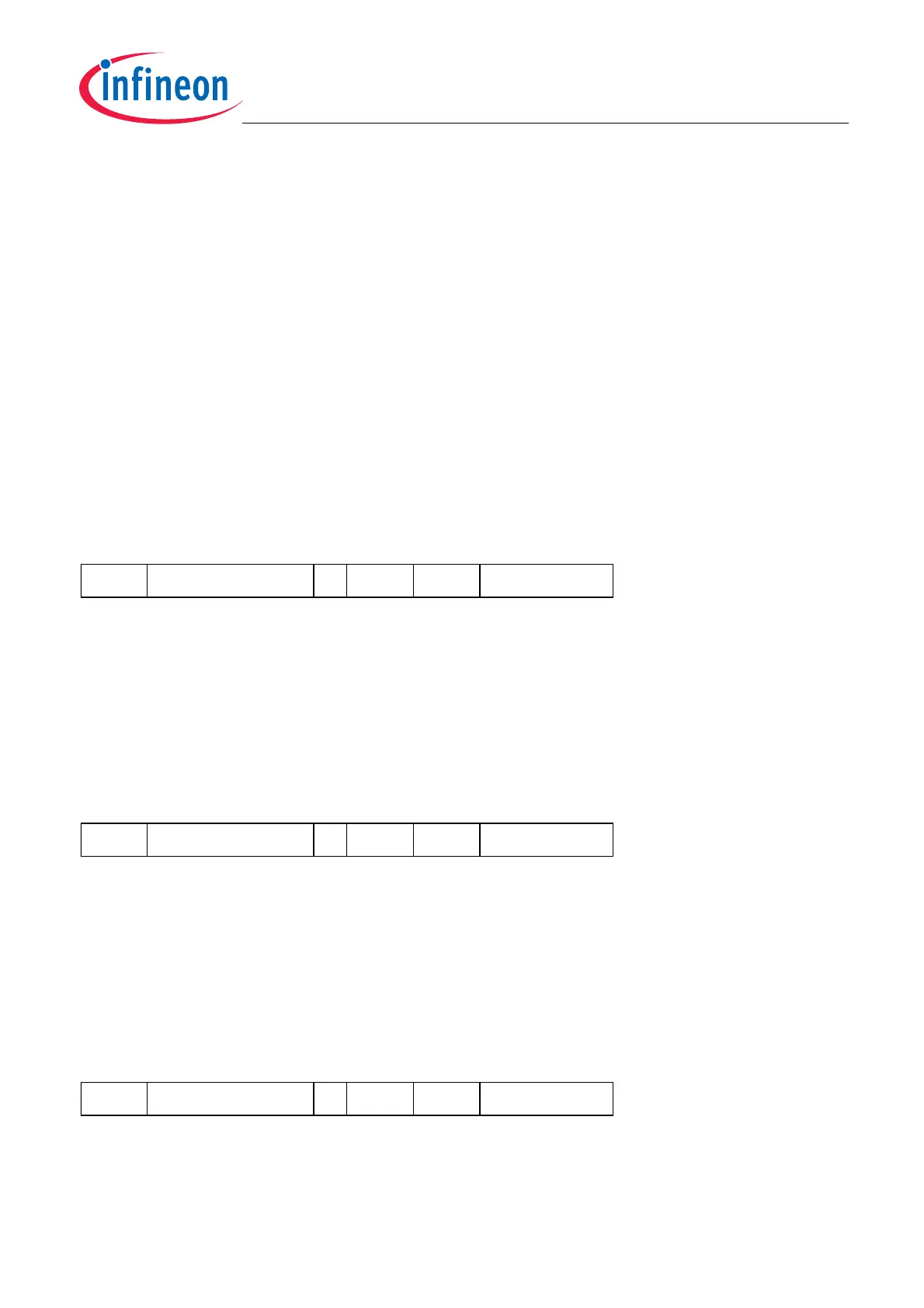
31
c
28 27
0E
H
18 17
n
16 15
b
12 11
a
8 7
B3
H
0
31
c
28 27
0D
H
18 17
n
16 15
b
12 11
a
8 7
B3
H
0
31
c
28 27
0C
H
18 17
n
16 15
b
12 11
a
8 7
B3
H
0

Infineon TriCore TC1.6P Specifications

General

Brand	Infineon
Model	TriCore TC1.6P
Category	Microcontrollers
Language	English