Mirion Technologies GEM-5 - Page 287

Counting Statistics
Gem-5 User’s Manual 271
The standard deviation can be calculated by solving the following integral:
Equation 9 Standard Deviation of Normal Distribution
∫
+∞
∞−
−= dx)x(G)x(
22
µσ
(9)
The probability for
x
to fall between
1
x
and
2
x
is defined by the following integral:
Equation 10 Probability of x to Fall Between x
1
and x
2
( )
∫
−
−
=<<
2
1
2
2
x
x
2
x
21
dxe
2
1
)xxx(P
σ
µ
σπ
(10)
With
σµ −=
1
x
and
σµ +=
2
x
the integral from Equation 10 is known as two
tailed Gaussian integral and gives the probability that a point lies within the given
number of σ from the mean μ.
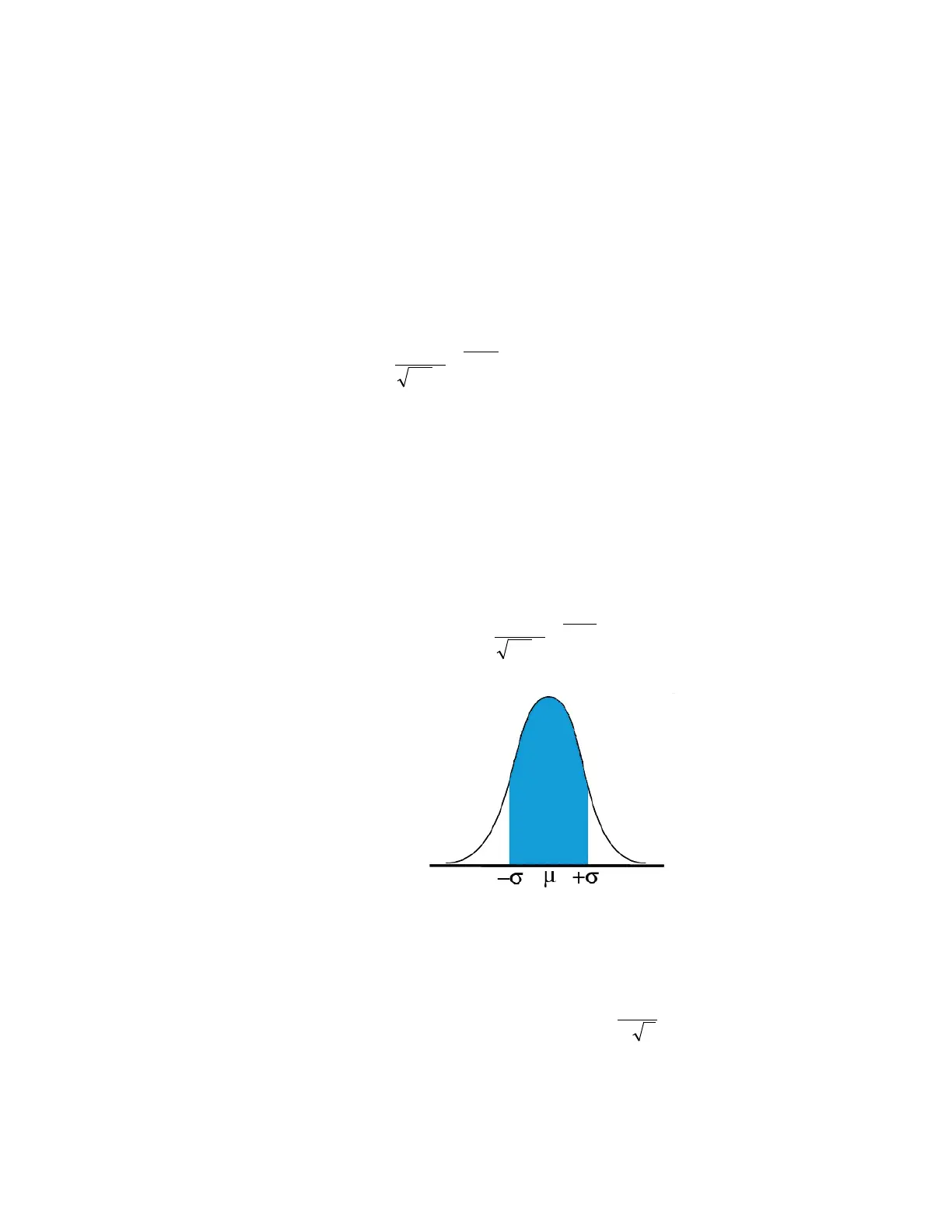
An individual observation from a normal distribution has a probability of 68% of
falling within ±1σ of mean, 95% of falling within ±2σ of mean and 99.7% of falling
within ±3σ of mean.
Equation 11 Two-Tailed Probability
( )
∫
+
−
−
−
−
=+<<−
σµ
σµ
σ
µ
σπ
σµσµ
dxe
2
1
)x(P
2
2
2
x
tailed2
(11)
Figure 128: Two-tailed distribution
In a special case when
0= µ
and using the substituition
2
x
t
σ
=
in Equation 11, the two-
tailed probability can be written in the following form: