GUI Reference
R&S
®
ZNB/ZNBT
294User Manual 1173.9163.02 ─ 55
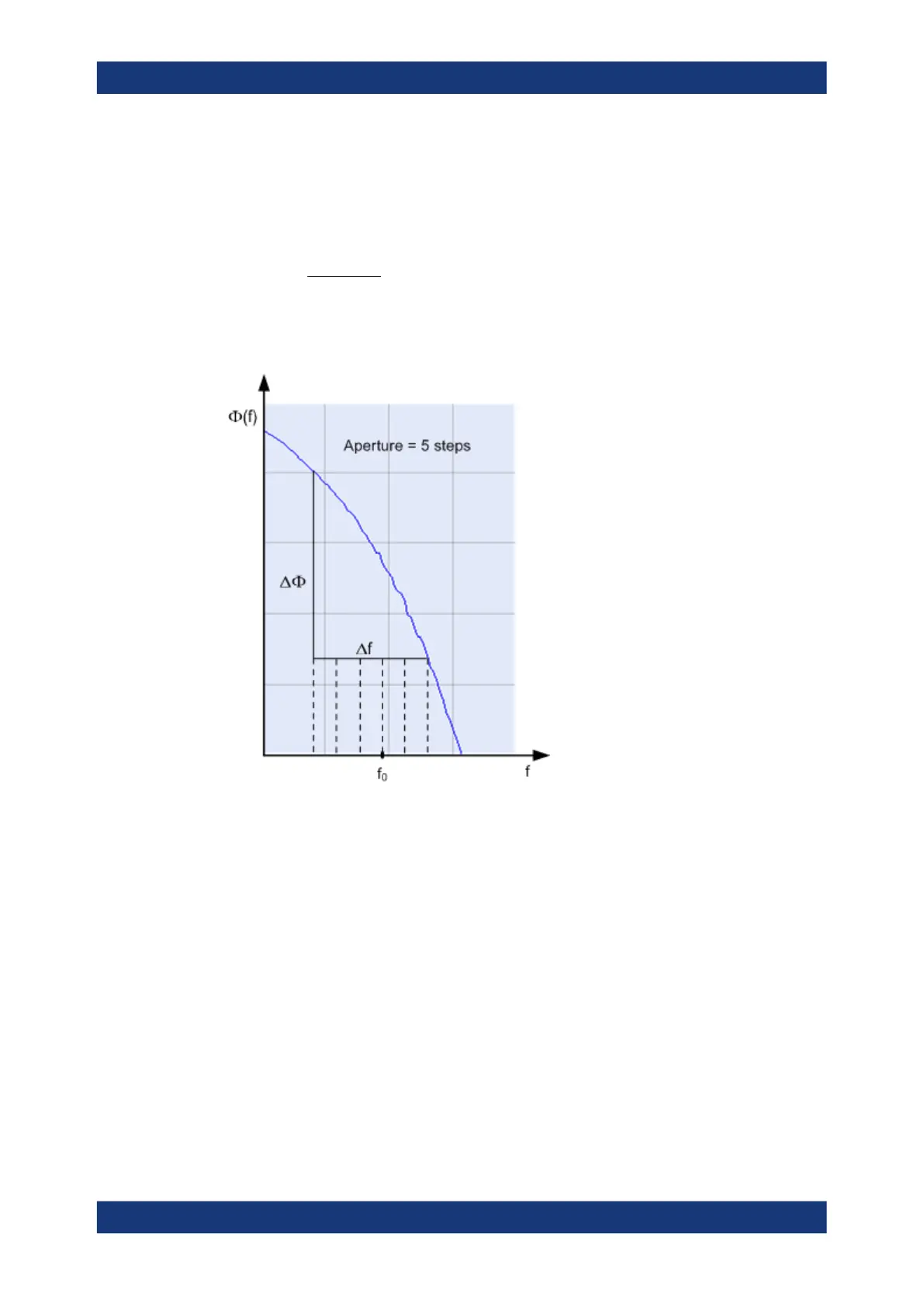
Aperture Points
Defines an aperture Δf for the (group) "Delay" calculation. The value is entered as
number of "Aperture Points" (i.e. sweep steps).
Properties: The delay at each sweep point is computed as:
where the aperture Δf is a finite frequency interval around the sweep point f
0
and the
analyzer measures the corresponding phase change ΔΦ.
Calculation of Δf and ΔΦ
With n sweep steps the delay at sweep point no. m is calculated as follows:
●
If n is even (n = 2k), then Δf (m) = f (m+k) – f (m–k) and ΔΦ(m) = ΔΦ (m+k) – ΔΦ
(m–k).
●
If n is odd (n = 2k+1), then Δf (m) = f (m+k) – f (m–k–1) and ΔΦ (m) = ΔΦ (m+k) –
ΔΦ (m–k–1).
The calculated phase difference (and thus the group delay) is always assigned to the
frequency point no. m.
For linear sweeps, if the number of aperture steps is odd, then the center of the aper-
ture range is [f (m+k) + f (m–k–1)] / 2 = f (m–1/2). I.e. the center is half a frequency
step below the sweep point f (m). Hence, toggling from even to odd numbers of aper-
ture steps and back can virtually shift the group delay curve towards higher/lower fre-
quencies. It is recommended, to use even numbers of aperture steps, especially for
large frequency step sizes.
The delay calculation is based on the already measured sweep points and does not
slow down the measurement.
Format Softtool

 Loading...
Loading...